Dinámica de los movimientos rectilíneos

Definamos primero unos conceptos básicos de la cinemática: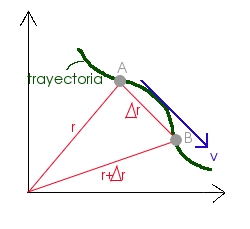

vector posición (r): La posición de un punto P viene dada por sus coordenadas en el sistema que se toma de referencia. Si una varía podemos decir que está en movimiento respecto al sistema. Se puede determinar mediando un vector origen en (0,0) y extremo en P. Estos conceptos de reposo y movimiento son relativos a los ejes que hemos tomado arbitrariamente como referencia, sin entrar en la cuestión de considerar si estos ejes, a su vez, se mueven o no respecto al sistema (como en el típico caso de viajar en coche. Uno dentro del coche no se mueve respecto al coche, pero sí se mueve respecto a un observador desde fuera).

Trayectoria: Al moverse P, el extremo del vector de posición describe la trayectoria. Por lo tanto, describe el lugar geométrico de las sucesivas posiciones que el punto va ocupando a lo largo del tiempo.

Espacio recorrido (s): Suma de las longitudes de todos los tramos recorridos por ese punto en el intervalo de tiempo considerado. Dado mediante el conocimiento de s=f(t ) (es decir, s es una función del tiempo) que da, en cada instante, el espacio recorrido.

Aristóteles nos dijo que todo lo que se mueve es movido por algo, y llegamos a la conclusión de que cualquier movimiento exige la acción de una fuerza. Newton demostró que no siempre era así y determinó la relación fuerza-movimiento en cada uno de los siguientes casos para el movimiento rectilíneo (y en el siguiente artículo para el movimiento circular).

Dinámica del movimiento rectilíneo y uniforme (MRU):

Como en este movimiento no existen ni aceleración radial ni aceleración tangencial, se cumplirá que: F = m·a = m·0 = 0 (segunda ley de newton). Es decir:

Para que exista movimiento rectilíneo y uniforme, sobre el cuerpo no ha de actuar fuerza alguna o, en el caso de que actúen varias formando un sistema, la resultante ha de ser nula.

Como a=0 —> Δs = |Δr|. Por lo tanto: v_media= Δs/Δt –> v=s/t –>s = v·t.

Suele afirmarse frecuentemente que las fuerzas instantáneas producen movimientos rectilíneos y uniformes. Esto ha de entenderse admitiendo que tal movimiento se produce, en realidad, después del brevísimo tiempo de actuación de la fuerza (diferencial, casi instantáneo). Durante ese tiempo de actuación, según el principio fundamental de la dinámica de traslación, necesariamente se originará una aceleración.

Dinámica del movimiento rectilíneo uniformemente acelerado (MRUA):

En este caso, como el movimiento es rectilíneo, existe únicamente una aceleración tangencial (la centrípeta se reserva para los movimientos circulares). Y como es un movimiento uniformemente acelerado entendemos que la aceleración es constante.

Así pues: F = m·a_t = constante.

Al ser la masa una magnitud escalar, se entiende que la fuerza resultante tendrá la misma dirección que la aceleración tangencial; ésta, a su vez, coincide con la de la velocidad.

Para que exista movimiento rectilíneo uniformemente acelerado sobre el cuerpo ha de efectuar una fuerza constante en la misma dirección de la velocidad. Si los sentidos de la fuerza y de la velocidad coinciden, el movimiento será uniformemente acelerado, en caso contrario se producirá una deceleración (aceleración negativa).

Como a = δv/δt –>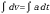 –> v=at+K –> v=v_o+at (1).

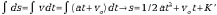–> s=s_o + v_ot + 1/2·at² (2).

(1) + (2) = v²-v_o² = 2as (3).