Ley de Stokes
El movimiento de un cuerpo en un medio viscoso es influenciado por la acción de una fuerza viscosa, Fv, proporcional a la velocidad, v, es definida por la relación Fv = bv, conocida como Ley de Stokes. En el caso de esferas en velocidades bajas Fv = 6pηrv, siendo r el radio de la esfera y η el coeficiente de viscosidad del medio. Si una esfera de densidad mayor que la de un líquido fuese soltada en la superficie del mismo, en el instante inicial la velocidad es cero, pero la fuerza resultante acelera la esfera de forma que su velocidad va aumentando pero de forma NO uniforme.
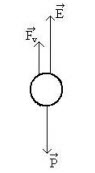
Se puede verificar que la velocidad aumenta no uniformemente con el tiempo pero alcanza un valor límite, que ocurre cuando la fuerza resultante fuese nula. Las tres fuerzas que actúan sobre la esfera están representadas en la figura 1 y son además e la fuerza viscosa, el peso de la esfera, P y el empuje, E. Igualando la resultante de esas tres fuerzas a cero obtenemos la velocidad límite VL.
Donde ρ y ρ’ son las densidades de la esfera y del medio respectivamente y g es la aceleración de la gravedad (9,81 cm s-2).
Figura 1. Fuerzas que actúan en una esfera en un medio viscoso.
El objetivo de este experimento es investigar el movimiento de una esfera en un medio viscoso (glicerina con agua) y determinar la viscosidad de la mezcla y el porcentual de agua en la glicerina.
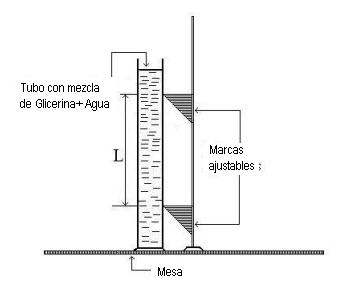
Emplearemos un tubo de vidrio con una escala graduada, en la posición vertical, conteniendo la mezcla (Figura 2). Como se trata de un fluido viscoso, al moverse por el mismo, la esfera causa un movimiento que afecta la fuerza viscosa
Para tener en cuenta este efecto se considera la corrección de Ladenburg que depende del radio de la esfera, del radio del tubo y de su altura. Así, la fuerza viscosa en el tubo, en realidad debe ser escrita como F»v = K(6πηrv), donde K es el factor de Ladenburg: K = (1+2,4r/A)(1+3,3r/H), donde A y H son respectivamente el radio del tubo y la altura total del fluido en el tubo
Por tanto la velocidad corregida es:
Siendo VL la velocidad que de hecho se mide y que está dada por la ecuación vL = (2/9) [(ρ – ρ’)/η] g r2
Material Utilizado
Tubo de vidrio con glicerina, soporte con marcas graduadas, conjunto de esferas, paquímetro, micrómetro, cronómetro y termómetro de mercurio.
Procedimiento y tratamiento de los datos
El arreglo experimental debe ser montado conforme mostramos en la figura a continuación. La velocidad límite será determinada experimentalmente a partir de la distancia entre las marcas ajustables, medida con una regla y el tiempo de recorrido entre las marcas medido con un cronómetro. Serán utilizadas esferas de acero con diámetro variado de 1 a 6 mm. La densidad del acero es ρa = 7.82 g/cm3 y la de la glicerina a 20ºC, ρg = 1.26 g/cm3. La viscosidad de la glicerina pura a 20ºC y η = 14.9 g cm-1 s-1 (1 g cm-1 s-1 = 1 Poise).
Antes de iniciar el experimento, debemos hacer un cálculo del factor de correlación de Landenburg para cada esfera, colocando los resultados en una tabla que deberá contener también columnas para el tiempo de caída de cada esfera, t, y la velocidad medida, VL y la velocidad corregida VC.
Rellenamos la tabla y a medida que el experimento va siendo realizado vamos reflejando los datos en un gráfico VL x r2 . En ese mismo gráfico colocamos también VL x r2. Obtenemos a partir del gráfico apropiado el coeficiente de viscosidad y su error.
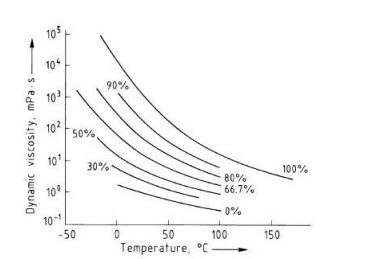
Determinamos la temperatura del líquido y consultando el gráfico estimamos la concentración del agua en la glicerina.
Principales cuidados:
1 – Es importante estimar el espacio necesario para alcanzar la velocidad límite, a partir de la superficie de la glicerina antes de posicionar los marcadores.
2 – Hacer repetidas medidas de tiempo de caída de las esferas para disminuir el error, principalmente para las esferas mayores.
3 – Retiramos cada esfera luego de cada medida
4 – No arroje las esferas y utiliza una pinza para colocarlas en la superficie del líquido y así minimizar su velocidad inicial
Viscosidad dinámica de la mezcla glicerina-agua. Las concentraciones son dadas en porcentaje de masa de glicerina. 1mPa s = 10-3 Pa s.