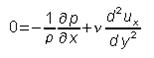Flujo Laminar
Debido a la presencia del término no lineal de advección |u|·|V| |u| en la ecuación de Navier-Stokes, se conocen muy pocas soluciones exactas de la misma. En general, este tipo de soluciones sólo son posibles cuando los términos no lineales son idénticamente nulos.
Un ejemplo de este tipo es el flujo entre placas paralelas completamente desarrollado. Al decir completamente desarrollado, nos referimos al flujo en una región lejos de la frontera de entrada o salida a las placas, donde la velocidad del flujo puede cambiar de signo debido a la formación de capas límite.
Dentro de esa zona de entrada, cuya longitud puede ser varias veces mayor a la distancia entre las placas, la velocidad no será paralela a las placas, por lo cual los términos no lineales no serán despreciables. Por el contrario, consideraremos un flujo estacionario completamente desarrollado entre placas paralelas infinitas separadas una distancia 2b.
El flujo será generado por una combinación de un gradiente en la presión impuesto de manera externa (por ejemplo sostenido con una bomba) y el movimiento de la placa superior a velocidad constante U. Sea el eje x horizontal y paralelo a la velocidad de flujo, y sea y el eje vertical perpendicular a las placas.
Si suponemos que el flujo es bidimensional, la velocidad del mismo no puede depender de la otra coordenada horizontal z. Las características del flujo deben ser invariantes a lo largo de la dirección x, por lo tanto la componente vertical de la velocidad debe verificar
Pero además sabemos que uy=0 en y=0, por lo cual deducimos que uy=0 en todo punto, lo cual es consistente con la hipótesis de flujo paralelo a las placas. Las ecuaciones de conservación del momento del fluido quedan entonces como:
La ecuación de conservación de momento vertical nos dice que la presión p no puede depender de la coordenada vertical y. Por lo tanto, en la ecuación de conservación de momento horizontal, el primer término sólo puede depender de x, mientras que el segundo término sólo puede depender de y. La única manera de satisfacer esto es que ambos términos sean constantes, lo cual implica que la presión varía linealmente a lo largo del canal. Integrando dos veces respecto a y la conservación de momento horizontal obtenemos:
donde hemos sustituido la derivada parcial de la presión por una derivada total dp/dx porque p sólo depende de x. Las constantes de integración A y B se pueden determinar como sigue. La condición de velocidad nula en la placa inferior ux=0 en y=0 requiere B=0. La condición de borde de velocidad ux=U en y=2b por otro lado, requiere
Por lo tanto, el perfil de velocidades del flujo queda como:
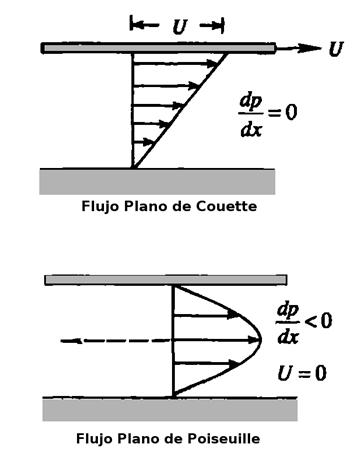
Dos casos particulares de este tipo de flujo laminar, ilustrados en la figura de abajo, son el flujo plano de Couette y el flujo plano de Poiseuille.
El caso del flujo generado solamente por el movimiento de la placa superior, sin un gradiente externo de presión impuesto, se llama flujo plano de Couette. En ese caso el perfil de velocidades del fluido se reduce a un perfil lineal, de la forma:
Entonces la magnitud del esfuerzo cortante del fluído para este tipo de flujo se calcula como:
o sea que su valor es constante en todo el canal.
Por otro lado el flujo entre dos placas estacionarias impuesto por un gradiente externo de presión se llama flujo plano de Poiseuille. En este caso el perfil de velocidades del flujo se reduce a:
Por lo que en este caso la magnitud del esfuerzo cortante del fluído queda como:
Lo que muestra que en este caso el esfuerzo cortante se distribuye linealmente en la dirección vertical del canal, con una magnitud absoluta máxima de b(dp/dy) en la superficie de las placas.
Es interesante notar que se puede probar que estos resultados de gradiente de presión constante y esfuerzo cortante distribuido linealmente son generales para el flujo completamente desarrollado entre placas paralelas, valen no solo para flujos laminares sino también para flujos turbulentos generados en condiciones de contorno similares.