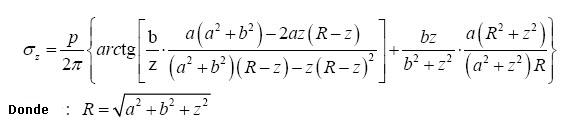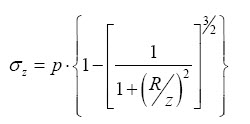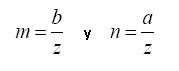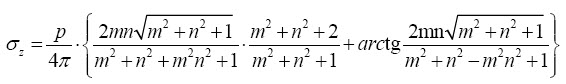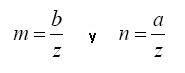Mecánica del suelo – Bulbos de Tensión

Distribución de tensiones debido a la aplicación de cargas

σ₀ = tensión debida al peso propio del suelo;

Δσ₁ = alivio de la tensión debido a la excavación;

Δσ₂ = tensión inducida por la carga “q”.

Al aplicarse una carga en la superficie de un terreno, en un área bien definida, la adición de tensión a cierta profundidad no se limitan a la proyección del área cargada. En las laterales del área cargada también ocurren aumentos de tensión, que se suman a los anteriores debido al peso propio.

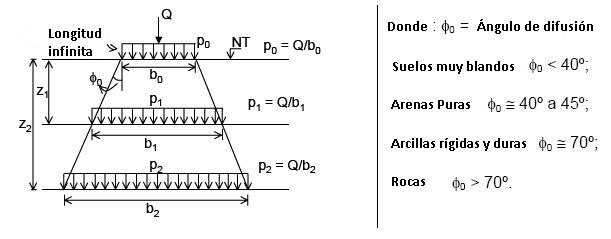
a) Tensiones de difusión o hipótesis simple

Una práctica corriente para estimar el valor de las tensiones en cierta profundidad consiste en considerar que las tensiones se difunden según áreas crecientes, pero siempre manteniéndose uniformemente distribuidas.

Este método debe ser comprendido como una estimativa a groso modo, pues las tensiones en una determinada profundidad no son uniformemente distribuidas, pero se concentran en las proximidades del eje de simetría del área cargada, presentando la forma de una campana.

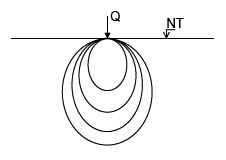
b) Bulbo de Tensiones

Se denominan isobaras de tensión a las curvas o superficies obtenidas enlazándose los puntos de la misma tensión vertical. Este conjunto de isobaras forma lo que se da en llamar “bulbo de tensiones”.

c) Distribución basada en la teoría de la elasticidad

Considera al suelo como un material:

• Homogéneo: iguales propiedades en todos los puntos
• Isotrópico: Iguales propiedades en todas direcciones
• Elástico¹: Obedece la Ley de Hooke, σ = E x ε (tensiones proporcionales a las deformaciones).

¹ Régimen elástico: Las tensiones crecen linealmente con las deformaciones y el cuerpo recupera la forma y el volumen iniciales al cesar la acción de las fuerzas.

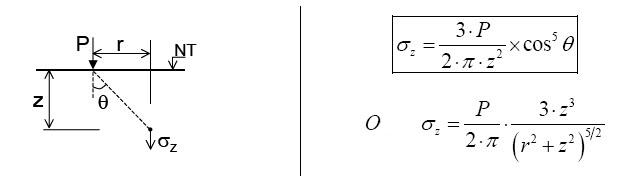
1. a. Soluciones de Boussinesq

La ecuación de Boussinesq determina las adiciones de tensiones verticales debidas a una carga puntual aplicada en al superficie.

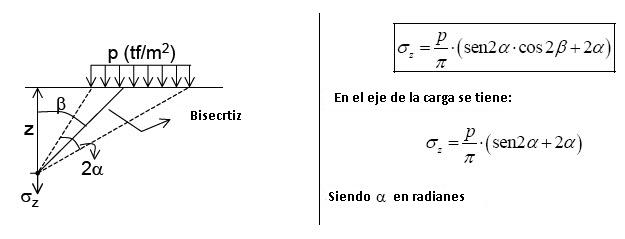
1. b. Soluciones de Caarothres

Determina las adiciones de tensiones verticales debidas a una carga uniformemente distribuida a lo largo de una franja de longitud infinita y ancho constante.

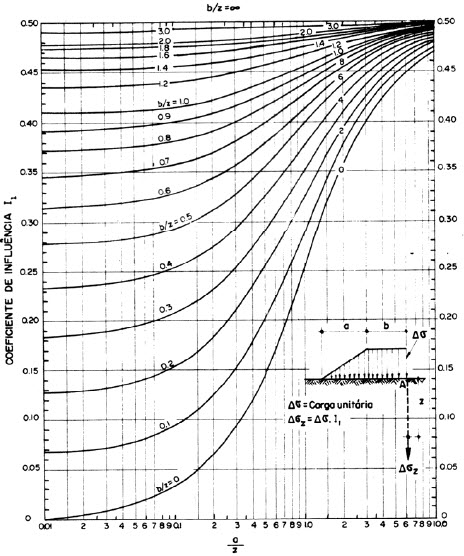
1. c. Soluciones de Steinbrenner

Steinbrenner construyó un gráfico integrando la fórmula de Boussinesq que permite la determinación de σ_z a una profundidad z debajo del vértice A de un rectángulo de lados a y b (a > b), uniformemente cargado por una tensión p.

El ábaco de Streinbrenner es la solución gráfica de la siguiente ecuación:

Para el cálculo de cualquier otro punto, se divide el área cargada en rectángulos con una arista en la posición del punto considerado y se calcula separadamente el efecto de rectángulo. σ_z será la suma de las acciones de cada una de las áreas.

1. d. Fórmula de Love

Determina la adición de tensión en puntos a lo largo de una vertical pasando por el centro de un área circula uniformemente cargada.

Donde R es el radio del área cargada y z es la profundidad considerada

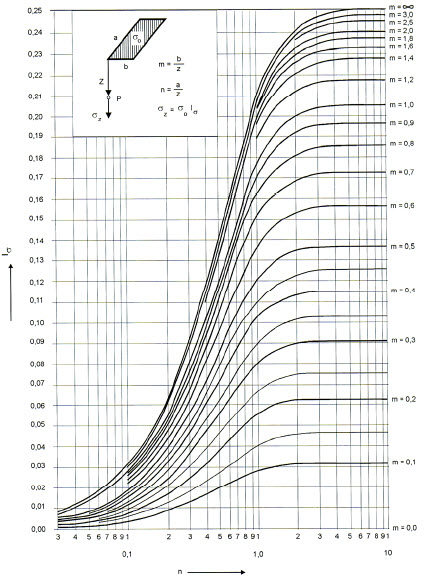
1. e. Ábaco de Newmark

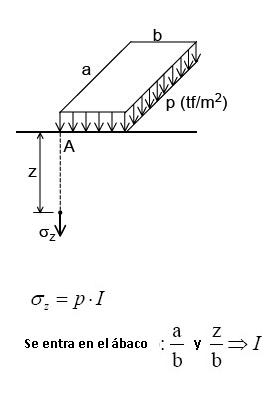
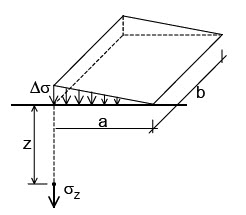
Determina σ_z a una profundidad z debajo de una vertical pasando por la arista del área rectangular. Son definidas las siguientes relaciones con los parámetros de m y n.

En función de estos parámetros, la solución de Newmark es:

Se considera la tensión como una función de los parámetros m y n y toda la expresión por encima puede ser tabulada de forma que σ_z = p.I , siendo que I se encuentra tabulado.

Para el cálculo en cualquier otro punto, se divide el área cargada en rectángulos con una arista en la posición del punto considerado y se calcula separadamente el efecto de rectángulo. σ_z será la suma de las acciones de cada una de las áreas.

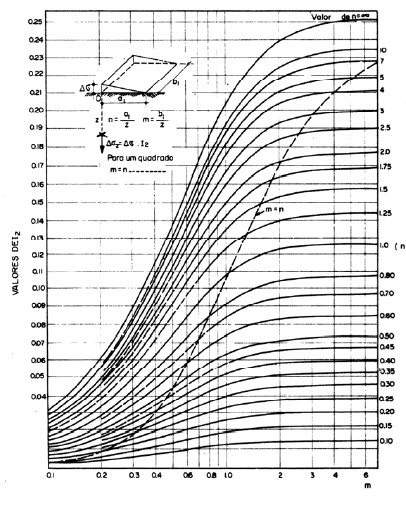
1. f. Gráfico de Fadum

Permite determinar el aumento de tensión vertical σ_z bajo una carga triangular de largo infinito.

Con las indicaciones de la figura y el gráfico de Fadum, se obtiene:

Siendo: Δσ =γ × h

Donde I es un coeficiente dado en función de dos parámetros m y n que de acuerdo con la figura son:

1. g. Gráfico de Osterberg

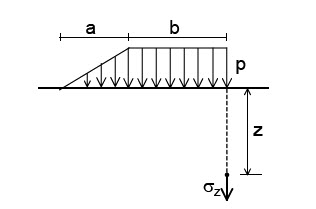
Permite calcular el aumento de tensión debido a una carga en forma de trapecio rectangular, infinitamente largo.

Con las indicaciones de la figura y el gráfico de Osterberg, se obtiene:

Ábaco de Steinbrenner

Ábaco de Newmark

Abaco de Fadum

Ábaco de Osterberg