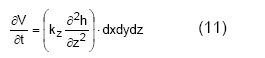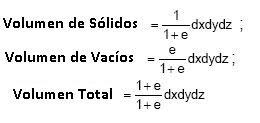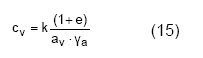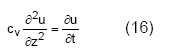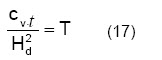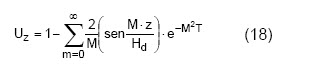Mecánica de Suelos – Deducción de la Teoría de Densificación de Terzaghi
El objetivo es determinar, para cualquier instante de tiempo y en cualquier posición de la capa que se esté densficando, el grado de densificación, o sea las deformaciones, los índices de vacíos y las tensiones efectivas y las presiones neutras correspondientes.
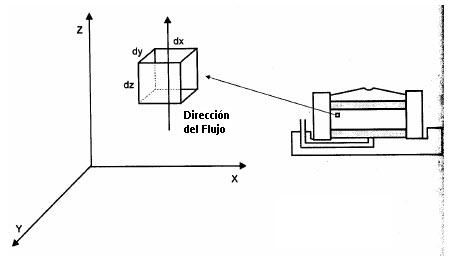
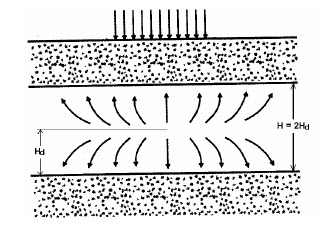
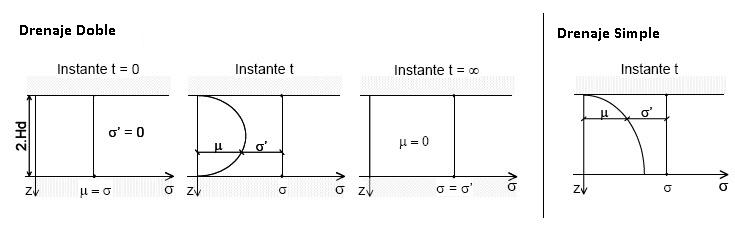
Consideremos el elemento del suelo sometido al proceso de densificación indicado en la figura a continuación:
El flujo tridimensional en un suelo saturado, sin variación volumétrica está dado por:
En la densificación existe variación de volumen y se admite que el flujo solo ocurre en una dirección, la vertical, desde que el agua y las partículas sólidas son consideradas incompresibles. La ecuación del flujo en este caso será:
La variación del volumen del suelo está expresada en términos de variación de su índice de vacíos, conforme vemos a continuación:
Entonces la variación del volumen con el tiempo está dada por:
Donde
Es igual al volumen de sólidos que no varía con el tiempo
Igualándose (12) y (11) obtenemos:
Solo la carga que excede la hidroestática provoca flujo. Por tanto, la carga h puede ser substituida por u dividida por el peso específico del agua (γa). Vimos también en la ecuación (9) que de = av.du. Entonces tenemos:
La parcela
Refleja características del suelo tales como permeabilidad, porosidad y compresibilidad. Por ello, a ella se le da el nombre de coeficiente de densificación, cv.
Entonces la ecuación diferencial de la densificación asume la siguiente expresión:
La ecuación (16) expresa la variación de la presión neutra, a lo largo de la profundidad, en el correr del tiempo. La variación de presión neutra está asociada a la variación de las deformaciones.
Condiciones de contorno para la solución de la ecuación diferencial de densificación unidimensional
a) Existe completo drenaje en los dos extremos de al muestra
- Para z = 0 y z = 2Hd ==> u0 = 0 (drenaje en la cima y en la base)
b) La sobrepresión neutra inicial, constante a lo largo de toda la altura, es igual al aumento de presión aplicada inicialmente (t=0) toda carga se transfiere hacia el agua (uo = uinicial).
En al integración de la ecuación diferencial (16) la variable tiempo “t” aparece siempre asociada al cv y a mayor distancia de flujo, o sea:
El símbolo “T” se denomina factor tiempo. T es adimensional, t es expresado en segundos, Hd en cm y cv en cm2/s.
El resultado de la integración de la ecuación (16) para las condiciones de contorno encima definidas está dado por al siguiente expresión:
Donde
Expresa el grado de densificación a lo largo de la profundidad “z”.
La expresión (18) revela que cuanto más próximo un elemento se encuentra de las facetas drenantes, más rápidamente las presiones neutras se disipan.
El factor Tiempo (T)
Para el problema de densificación unidimensional, las condiciones límite son las siguientes:
a) Existe completo drenaje en las dos extremidades de la muestra
b) La presión neutra inicial en t=0 es constante a lo largo de toda la altura, siendo μ = σ. Y para t= ∞ se tiene que σ » = σ, constante a lo largo de la altura.
c) En una extremidad z = 0 y en la otra z= 2⋅Hd, siendo Hd la mitad del espesor de la muestra H. Hd indica la mayor distancia de flujo de la muestra.
La figura a continuación muestra la solución de la ecuación (18) para diversos tiempos luego de la aplicación de la carga. Ella indica como la presión neutra se encuentra a lo largo del espesor para diversos instantes luego de la carga, a partir de curvas correspondientes a diversos valores del Factor tiempo (T). Esas curvas son llamadas isócronas (igual tiempo). Las curvas también muestran como las deformaciones ocurren mucho más rápidamente en las proximidades de las facetas de drenaje que al interior de la capa.
Porcentaje de Densificación Uz
El asentamiento que se forma en la superficie del terreno es el resultado de la sumatoria de las deformaciones de los diversos elementos a lo largo de la profundidad. Por tanto si calculamos la media de los grados de densificación a lo largo de la profundidad z, obtendremos el grado de densificación medio, que está dado por la ecuación (19).