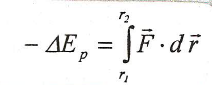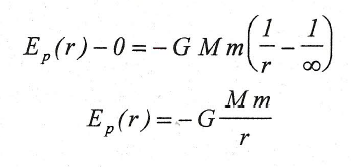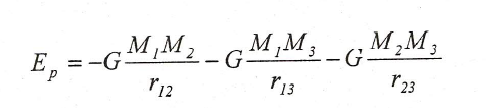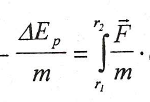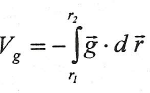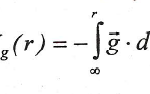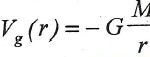Energía potencial gravitatoria

Como ya vimos el día anterior, el campo de fuerzas gravitatorio es conservativo, por tanto es posible definir una función escalar dependiente de la posición: la energía potencial gravitatoria, la cual denotaremos por Ep, cuya disminución entre dos puntos es igual al trabajo realizado por el campo para trasladar una partícula entre dichos puntos:

Si en la fórmula anterior, sustituimos la fuerza gravitatoria por su definición obtenemos lo siguiente:

Esta ecuación nos da la diferencia de energía potencial entre dos puntos. Para hablar de la energía potencial gravitatoria en un punto es necesario en primer lugar, fijar arbitrariamente su valor en una posición previamente convenida. Por ejemplo, resulta muy útil tomar Ep=0 cuando las masas se encuentran infinitamente alejadas, o sea, si r=∞; en tal caso, si en la última ecuación obtenida, sustituimos Ep(r1)=0 y r1=∞, la energía potencial gravitatoria de la masa m cuando se encuentre a una distancia r de M será:

La cual nos permite saber el trabajo realizado por la fuerza gravitatoria para trasladar la masa m desde el infinito hasta una distancia r de la masa M.

Es más, podemos decir que esta última ecuación expresa la energía potencial del sistema compuesto por dos masas, M y m, separadas una distancia r. En el caso de sistemas más complejos, la energía potencial gravitatoria incluye un término como el de la última ecuación para cada pareja de masas. Por tanto, si consideramos tres masas, puesto que podemos establecer tres parejas, tendríamos:

donde rij es la distancia entre la masa Mi y Mj.

POTENCIAL GRAVITATORIO

Vamos a introducir a partir de la primera fórmula que hemos dado para la energía potencial gravitatoria, un nuevo concepto: el potencial gravitatorio, que mide la disminución de energía potencial por unidad de masa. Por tanto, se obtiene al dividir el aumento de energía potencial entre m:

Esta expresión se denomina diferencia de potencial gravitatorio entre dos puntos y los denotamos por ∆Vg, y también lo podemos escribir como:

Es decir, la diferencia de potencial gravitatorio entre dos puntos es igual al trabajo, cambiado de signo, realizado por las fuerzas gravitatorias para trasladar la unidad de masa desde un punto al otro. En el caso de que, por convención, asignemos un valor potencial a un punto concreto, podemos definir el potencial gravitatorio en cualquier otro punto. Por ejemplo, tomemos Vg( r1=∞)=0, entonces obtendríamos:

Esta fórmula nos da el potencial gravitatorio en un punto situado a una distancia r de la masa M, que valdrá:

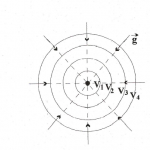
Por último, también hay que tener en cuenta que el potencial gravitatorio se representa mediante superficies equipotenciales. Para una masa puntual, consistirá en superficies esféricas concéntricas caracterizadas cada una de ellas por un valor potencial, como podemos ver en la siguiente imagen. Además, también podemos observar que las líneas de campo son perpendiculares en cada punto a las superficies equipotenciales.