Dinámica y cinemática de rotación

Si A y B se encuentran ligados a puntos fijos internos o externos y se aplican una fuerza sobre el sólido rígido se producirá un movimiento de rotación.

Al aplicar una fuerza F a un punto sólido (siempre que no corte el eje de giro) producirá un efecto análogo al que origina otra fuerza igual y paralela a ella y de sentido opuesto –> se las denomina par.

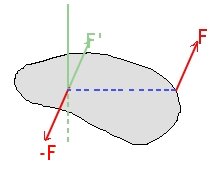
En un punto del eje actúan simultáneamente dos fuerzas opuestas F y -F, de direcciones paralelas a la primera y de igual valor a ella. En el eje las fuerzas se anulan de forma que sólo quedan las originales que dan lugar a la rotación.

cinemática:

Recordemos las bases de la cinemática del movimiento circular (de trayectoria circular):

• – El arco recorrido (ángulo): s=φ·R, donde R es el radio del círculo descrito. Las unidades que expresan la medida del arco s vienen condicionadas por las que miden la longitud del radio R. Este ángulo define la posición instantánea de cualquier partícula contenida en el cuerpo rígido y se mide desde un plano perpendicular al eje de rotación
• – La velocidad angular: v=ω·R. δs/δt=(δφ/δt)·R. Se representa por un vector axial cuya dirección es perpendicular al plano de giro y su sentido sigue la regla del tornillo.
• – La aceleración angular (tangencial): a_t=α·R. δv/δt=(δω/δt)·R
• – La aceleración normal: a_n=v²/R = (ω·R)²/R = ω²·R. Si el movimiento fuese circular uniforme la a=0. Por lo tanto también lo sería la a_t. Sin embargo, habría aceleración normal, ya que ésta tan sólo depende de ω y R.
• – La fuerza centrípeta: F_n=(mv²)/R = m·ω²·R. La existencia de un movimiento circular supone siempre la acción de una fuerza perpendicular a la dirección de la velocidad y con sentido hacia el centro de la curva descrita por el móvil.
• – La frecuencia: medida escalar de la velocidad de rotación.
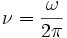
• – El período: es el inverso de la frecuencia y representa el tiempo que se tarda en dar una revolución completa. .

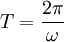Además de estos conceptos básicos, es importante entender que la rotación puede ser analizada desde diferentes marcos de referencia. Por ejemplo, un observador en reposo verá un objeto rotar a una cierta velocidad, mientras que un observador en movimiento verá el mismo objeto rotar a una velocidad diferente. Esto se conoce como la relatividad del movimiento de rotación.

En el estudio de la rotación, también se utilizan conceptos como el momento de inercia y el momento angular. El momento de inercia es una medida de la resistencia de un objeto a cambiar su estado de rotación. Depende tanto de la masa del objeto como de la distribución de esa masa alrededor del eje de rotación. Por otro lado, el momento angular es una medida de la cantidad de rotación que un objeto tiene. Es el producto del momento de inercia y la velocidad angular.

La energía cinética de rotación es otra cantidad importante en la dinámica de rotación. Es la energía que un objeto tiene debido a su rotación y se calcula como la mitad del producto del momento de inercia y el cuadrado de la velocidad angular.

Finalmente, es importante mencionar que la rotación puede ser causada por varios tipos de fuerzas, incluyendo la gravedad, las fuerzas electromagnéticas y las fuerzas nucleares. Estas fuerzas pueden causar que un objeto comience a rotar, cambie su velocidad de rotación o cambie la dirección de su eje de rotación.