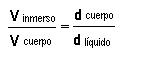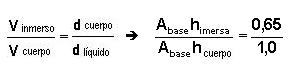Hidrostática – Principio de Arquímedes – Empuje

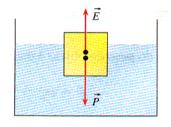
Cuentan los libros que el sabio griego Arquímedes (282-212 AC) descubrió mientras tomaba un baño, que un cuerpo inmerso en el agua se vuelve más liviano debido a una fuerza ejercida por el líquido sobre el cuerpo, vertical y hacia arriba que alivia el peso del cuerpo. Esa fuerza del líquido sobre el cuerpo se denomina empuje |E|.

 

Por tanto, en un cuerpo que se encuentra inmerso en un líquido, actúan dos fuerzas: la fuerza peso |P|, debida a la interacción con el campo gravitatorio terrestre y la fuerza empuje |E|, debida a su interacción con el líquido.

 

 

Cuando un cuerpo está totalmente inmerso en un líquido, podemos tener las siguientes condiciones:

 

• Si el permanece detenido en el punto donde fue colocado, la intensidad de la fuerza de empuje es igual a la intensidad de la fuerza peso (E=P);

 

• Si el objeto se hunde, la intensidad de la fuerza de empuje es menor que la intensidad de la fuerza peso (E < P); y

 

• Si el es llevado a la superficie, la intensidad de la fuerza de empuje es mayor que la intensidad de la fuerza peso (E > P) .

 

Para saber cual de las tres situaciones será la que ocurre, debemos enunciar el principio de Aquímedes:

 

Todo cuerpo sumergido en un fluido (líquido o gas) sufre, por parte del fluido, una fuerza vertical para arriba cuya intensidad es igual al peso del fluido desplazado por el cuerpo.

 

Sea V_f el volumen del fluido desplazado por el cuerpo. Entonces la masa del fluido desplazado está dada por:

 

m_f = d_fV_f

 

La intensidad del empuje es igual a la del peso de esa masa desplazada:

 

E = m_fg = d_fV_fg

 

Para cuerpos totalmente inmersos, el volumen del fluido desplazado es igual al propio volumen del cuerpo. En este caso, la intensidad del peso del cuerpo y del empuje son dadas por:

 

P = d_cV_cg e E = d_fV_cg

 

Comparando ambas expresiones observamos que:

 

* Si  d_c > d_f , el cuerpo desciende en movimiento acelerado ((F_R = P – E);

* Si d_c < d_f , el cuerpo sube en movimiento acelerado (F_R = E – P);

* Si d_c = d_f , el cuerpo se encuentra en equilibrio

 

Cuando un cuerpo más denso que un líquido está totalmente inmerso en este líquido, observamos que el valor de su peso, dentro de este líquido es aparentemente menor de la que en el aire. La diferencia entre el valor del peso real y del peso aparente corresponde al empuje ejercido por el líquido:

 

P_aparente = P_real – E

 

Ejemplo:

 

Un objeto con masa de 10 kg y volumen igual a  0,002 m³ se coloca  totalmente dentro del agua (d = 1 kg/L).

 

 

a)    Cual será el valor del peso del objeto?

b)    Cual es la intensidad de la fuerza de empuje que el agua ejerce en el objeto?

c)    Cual es el valor del peso aparente del objeto?

d)    Despreciando el rozamiento con el agua, determinamos la aceleración de objeto. (utilizamos g = 10 m/s2.)

 

Resoluciones:

 

a) P = mg = 10.10 = 100N

 

b) E = d_agua V_objeto g = 1.000 x 0,002 x 10 ==> E = 20N

 

c) P_aparente = P – E = 100 – 20 = 80N

 

d) F_R = P – E ==> a= 8,0 m/s² (se hundiría, porque P > E)

 

Fluctuación

 

Para un cuerpo fluctuando en un líquido, tenemos las condiciones a continuación:

 

1 – El se encuentra en equilibrio

E = P

2 – El volumen del líquido que el desplaza es menor que su volumen: V_desplazado < V_cuerpo

3 – Su densidad es menor que la densidad del líquido

d_cuerpo < d_líquido

4 – El valor del peso aparente del cuerpo es nulo:

P_aparente = P – E = O

 

La relación entre los volúmenes inmerso y total del cuerpo está dada por:

E = P ==> d_líquidoV_imerso g = d_cuerpoV_cuerpo g

Ejemplo:

 

Un bloque de madera (d_c = 0,65 g/cm³), con 20 centímetros de arista, fluctúa en el agua (d_agua = 1,0 g/c³). Determinamos la altura del cubo que permanece dentro del agua.

 

 

Resolución:

 

Como el bloque está fluctuando, tenemos que E = P y siendo que V = A_base h , expresamos que:

 

 

Como h_cuerpo = 20 cm, entonces h_inmerso = 13 cm