Dinámica Relativista
En el caso de grandes velocidades, las leyes de la Mecánica de Newton no están de acuerdo con los nuevos conceptos de espacio y tiempo. Solo cuando la velocidad es pequeña, los conceptos clásicos de espacio y de tiempo son válidos, la segunda ley de Newton.
![]()
No se altera con la transición de un sistema de referencia inercial para otro (se verifica el principio de la relatividad)
Para velocidades grandes, sin embargo, esta ley en su forma habitual (clásica), no es verdadera.
De acuerdo con la segunda Ley de Newton (fórmula de arriba) una fuerza constante que actúe en el cuerpo durante algún tiempo, puede transmitirle una velocidad tan grande cuanto se quiera. Pero en la realidad, la velocidad de la luz en el vacío es limitada y en ningunas condiciones un cuerpo se puede mover con una velocidad mayor que la de la luz en el vacío.
Es necesario un pequeño cambio en la ecuación del movimiento de los cuerpos para que se vuelva verdadera la afirmación para grandes velocidades de movimiento.
Pasemos previamente a la formulación de la segunda ley de la dinámica, utilizada por el propio Newton
![]()
donde
![]()
es el impulso (cantidad de movimiento) del cuerpo. En esta ecuación, la masa del cuerpo se consideraba independiente de la velocidad.
Es sorprendente que mismo en el caso de grandes velocidades la ecuación (5) no cambia de forma. Las modificaciones solo se refieren a la masa.
Cuando aumenta la velocidad del cuerpo, su masa no se mantiene consntante, pero aumenta. El aumento de la masa es tanto más acentuado cuanto más cerca la velocidad del cuerpo esté de la velocidad de la luz c.
La dependencia de la masa en relación a la velocidad puede calcularse a partir de la suposición de que la ley de la conservación del impulso es verdadera para las nuevas concepciones de espacio y tiempo. Los cálculos son demasiado complicados.
Solamente presentaremos aquí los resultados finales.
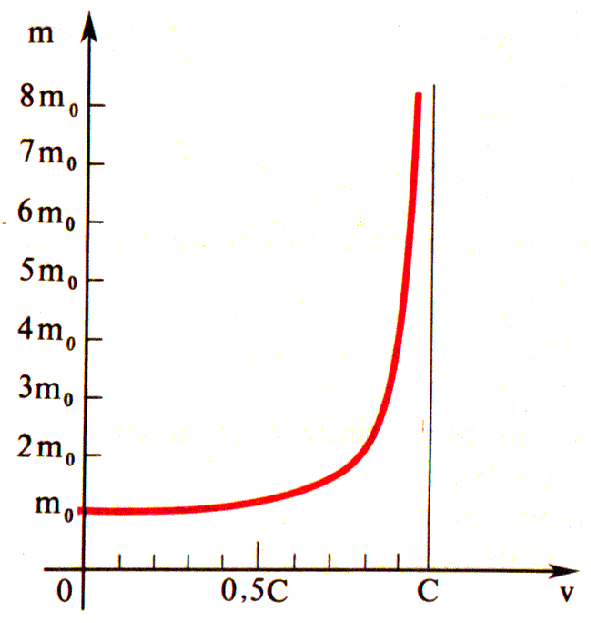
Fig. 5
Si designamos a través de m0 la masa del cuerpo en reposo, entonces la masa m de este mismo cuerpo en movimiento con velocidad v se define por la fórmula.
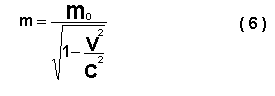
En la Figura 5 está representada la dependencia de la masa del cuerpo en relación a su velocidad.
Cuando la velocidad del movimiento es mucho menor que la de la luz, la expresión
![]()
Poco difiere de la unidad. Así para la velocidad de una nave espacial actual, v = 10 km/s, obtenemos
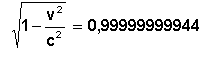
No es de admirarse, por ello que no se note el aumento de masa con el aumento de velocidad cuando comparamos pequeñas velocidades.
Pero las partículas elementales, en los actuales aceleradores de partículas cargadas, alcanzan velocidades enormes. Si la velocidad de una partícula fuese apenas 90 Km/s menor que la velocidad de la luz, entonces su masa aumentaría 40 veces.
Los aceleradores potentes de electrones pueden imprimir a estas partículas velocidades inferiores a la velocidad de la luz apenas en 35 – 40 m/s. En estas condiciones, la masa del electrón aumenta aproximadamente 2000 veces y se vuelve mayor que la del protón.
Para que este electrón se mantenga en una órbita circular es necesario que el campo magnético ejerza sobre él una fuerza 2000 veces mayor de la que se podría suponer, no considerando la dependencia de masa en relación a la velocidad.
Para calcular la trayectoria de partículas rápidas ya no se puede utilizar la mecánica de Newton.
De acuerdo con la relación (6), el impulso de un cuerpo es igual a:
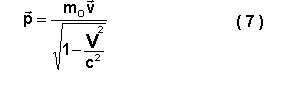
La ley fundamental de la dinámica relativista mantiene la forma anterior
![]()
Sin embargo, el impulso del cuerpo en este caso se define por la fórmula (7) y no por el simple producto.
![]()
De este modo, la masa que desde el tiempo de Newton, durante dos siglos y medio se consideraba invariable, en realidad depende de la velocidad.
La necesidad de utilizar la ecuación de movimiento relativista, cuando se calcula la aceleración de partículas cargadas, significa que la teoría de relatividad de nuestro tiempo, pasó a ser una ciencia estrechamente ligada a la ingeniería.
Las leyes de la mecánica de Newton pueden ser consideradas un caso particular de la mecánica relativista, siendo verdaderas cuando la velocidad del movimiento del cuerpo es mucho menor que la velocidad de la luz.
