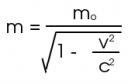Las leyes de Newton son tres que pretenden modelar la dinámica de una partícula.

Isaac Newton

Antes de comenzar daré algunas definiciones básicas:

fuerza: agente capaz de producir una variación en el estado de un cuerpo.

interacción: acción de unos cuerpos sobre otros –> suma vectorial de las fuerzas.

1 Newton: unidad de fuerza. Fuerza que hay que aplicar a 1kg de masa para que adquiera una aceleración de 1m/s2.

masa: es la medida de la cantidad de materia que resulta de su densidad y volumen conjuntamente: m=v·d.

peso: fuerza ejercida sobre una masa por el campo gravitatorio.

equilibrio: momento en el que la aceleración total del objeto es nula.


2º) Principio Fundamental de la Dinámica de Traslación:

El cambio de movimiento (cantidad de movimiento) es proporcional a la fuerza motriz que se le ha impreso, y sigue en la dirección de la línea recta en que se le imprimió la fuerza. O lo que es lo mismo, la fuerza que actúa sobre un cuerpo es igual a la derivada,respecto al tiempo, de su momento lineal.

Aquí introducimos una nueva magnitud, la cantidad de movimiento, definida como p=masa·velocidad. Actualmente también se la conoce como momento lineal. Al ser la masa una magnitud escalar y la velocidad una magnitud vectorial, el momento lineal ha de ser necesariamente vectorial de dirección y sentido las del vector velocidad. Su ecuación de dimensiones será: [p] = [m·v] = [m· s/t] = M·L·T-1 y por lo tanto sus unidades Kg·m/s2.

Si se modifica la velocidad de un cuerpo (modelado como una partícula) por la acción de una fuerza externa (ya sea en cualquiera de sus características vectoriales: valor, dirección y/o sentido), se modifica, en consecuencia, su momento lineal. Esta variación no es inmediata, sino que lleva instantes diferenciales de tiempo. Así pues podemos relacionar la variación de momento lineal con el tiempo y la fuerza de la siguiente forma:


F= δP/δt

Como P=m·v, F= δP/δt = δmv/δt y, teniendo en cuenta que a=δv/δt (como se estudia en cinemática), esto equivale a:

F = m·a

que es la otra forma de formular la Segunda Ley de Newton y la expresión propiamente conocida como Ecuación Fundamental de la Dinámica de Traslación.

De esta forma podemos reescribir el principio como:

Si sobre un cuerpo actúa una fuerza, o varias (cuya resultante no sea nula), adquiere una aceleración con valor directamente proporcional al de la fuerza aplicada e inversamente proporcional a la masa del cuerpo. Es decir: a = F/m.

Esta nueva expresión nos permite obtener la ecuación dimensional de la fuerza: [F] = M·L·T-2 y definimos su unidad como el Newton (N). También podemos hacer un estudio más exhaustivo de la masa. Ahora la masa viene definida como la relación constante que existe entre el valor de la fuerza aplicada a un cuerpo y la aceleración que adquiere con ella: m=F/a. Tenemos un concepto de masa dinámico y lo que conocemos como “cantidad de materia que posee un cuerpo” pasa a llamarse “masa en reposo” (m0). Newton suponía que la masa, al asociarla a la cantidad de materia, era una propiedad constante de los cuerpos pero recientes investigaciones demuestran que es una propiedad variable que relaciona la masa (m) con la velocidad de la partícula (v) y la velocidad de la luz en el vacío (c).

ecuación de la masa

En el mundo que conocemos, esta defición no se usa, pues no manejamos velocidades tan grandes como para que sea necesario tomarla en consideración.

Los sistemas en los que esta ley no se verifica se llaman no inerciales.

La primera ley de Newton es una consecuencia directa de ésta, pues es claro observar que cuando F=0 la partícula tendrá un movimiento rectilíneo uniforme de forma indefinida (o bien permanecerá en reposo si la velocidad es nula), ya que la aceleración deberá ser cero (pues la masa nunca puede ser cero). Este es el movimiento descrito como ‘movimiento por inercia’.




NOTA: Las variables en negrita son vectoriales, las variables sin negrita son escalares.