Sistemas de referencia -rectangular, cilíndrico y esférico-

Para ser capaz de analizar campos, e integrar en los espacios que toca, es imprescindible saber utilizar los diferentes sistemas de referencia, tanto el rectangular o cartesiano, el cilíndrico o el es esférico (o incluso algún cambio de variable de tu invención que te facilite los cálculos). Resulta demasiado complejo integrar una esfera usando un eje rectangular de coordenadas x, y, z, pues hay que descomponer los ángulos, mientras que de hacerlo en esféricas, con coordenadas r,θ,φ, sale más sencillo. Y lo mismo ocurre en caso de un cilindro con los ejes cilíndricos de coordenadas ρ, φ z.

¿Qué representa cada coordenada?

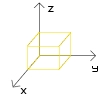Pues en cartesianas es sencillo porque son las que hemos usado toda la vida. Es, en perspectiva caballera, y el eje horizontal, z el vertical y x el eje que sale del papel.

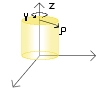En cilíndricas el eje vertical sigue siendo z, mientras que existe un eje radial que es ρ y otro circular, que representa el giro dibujado por un punto del cilindro para formarlo.

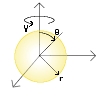
En esféricas θ representa el ángulo recorrido desde la vertical (0 en la vertical hacia arriba, π en el sentido hacia abajo), φ representa el ángulo girado igual que en cilíndricas (de 0 a 2π) y esta vez el radio de la esfera es r (no confundir con ρ que es el radio del cilindro).

En cada sistema de referencia existe un valor para el diferencial de longitud (δL), un valor para el diferencial de superficie (δS), un valor para el diferencial de volumen (δV) y un valor para el vector de posición (r). En cartesianas es obvio que una línea en dirección x, tendrá de longitud un diferencial de x (δx), en dirección y un diferencial de y (δy), en dirección z un diferencial de z (δz) y una línea en cualquier dirección tendrá de longitud la composición (suma) de dos o las tres anteriores. De la misma forma que una superficie cuyo vector normal está en dirección x tiene de lados δy y δz y el producto de ambos será el valor de la superficie, y así sucesivamente. En la siguiente tabla se recogen los valores de estos parámetros para cada sistema de referencia estudiado. Las variables en negrita y cursiva son vectoriales y únicamente definen la dirección y sentido de la magnitud por la que van multiplicadas.

	RECTANGULARES	CILÍNDRICAS	ESFÉRICAS
δL	(δx)x+(δy)y+(δz)z	(δρ)ρ+ρ(δφ)φ+(δz)z	(δr)r+r(δθ)θ+rsenθ(δφ)φ
δS	(δy)(δz)x+(δx)(δz)y+(δx)(δy)z	ρ(δφ)(δz)ρ+(δρ)(δz)φ+ +ρ(δρ)(δφ)z	r2senθ(δφ)(δθ)r+ +rsenθ(δφ)(δr)θ+r(δθ)(δr)φ
δV	(δx)(δy)(δz)	ρ(δρ)(δφ)(δz)	r2sen(δr)(δφ)(δθ)
r	xx+yy+zz	ρρ+zz	rr