Dinámica de los movimientos circulares

Nuevamente, igual que con los movimientos rectilíneos, destacamos dos casos:

Dinámica del movimiento circular uniforme:

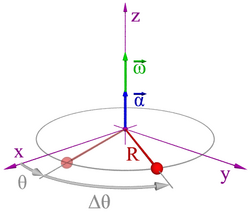
En este tipo de movimiento existe únicamente aceleración normal constante (centrípeta: a=v²/r), la aceleración tangencial (con sentido tangente a la trayectoria en cada punto) será nula. Ésta aceleración tendrá que ser originada también por una fuerza constante dirigida en la misma dirección y sentido (recordamos que F=m·a), es decir, perpendicular a la dirección de la velocidad y con sentido hacia el centro de la circunferencia. Su valor vendrá dado por: F = m·a_normal = m·v²/r. La velocidad angular viene representada por un vector axial cuya dirección es perpendicular al plano de giro y su sentido sigue la regla del tornillo. .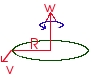

Por lo tanto, v= ω²·r y F = m·v²/r = m·ω²·r. A esta fuerza se le llama fuerza normal o fuerza centrípeta.

Dinámica del movimiento circular uniformemente acelerado:

En este caso existen las dos aceleraciones, la tangencial, constante, y la normal, variable. Por lo tanto, en principio, hemos de admitir la necesidad de dos fuerzas: una fuerza tangencial, constante y en la misma dirección que la aceleración tangencial y otra fuerza normal o centrípeta, variable, perpendicular a la dirección de la velocidad y con sentido hacia el centro de la circunferencia.

Ambas fuerzas, al ser simultáneas y actuar sobre un mismo punto, forman un sistema que, evidentemente, puede ser sustituido por una sola fuerza resultante: .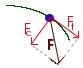

Ésta, según lo expuesto, deberá descomponerse en dos componentes rectangulares según estas características:

– La que actúe en la dirección de la velocidad será de módulo constante.

– La que actúe perpendicularmente a la velocidad y con sentido hacia el centro de la circunferencia será variable y su valor en cada instante corresponderá a la expresión. m·v²/r. El módulo de la fuerza resultante vendrá dado (por la ley de Pitágoras): 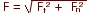.