Estática del punto material y cuerpo rígido
El equilibrio de los cuerpos es más común en nuestro cotidiano de lo que podemos imaginar. Los móviles de nuestro cuarto, las edificaciones y nosotros mismos, ahora, leyendo este texto, estamos sometidos a un conjunto de fuerzas que están cancelándose y contribuyendo para el estado de equilibrio.
La estática es el área de la mecánica que estudia el equilibrio de los cuerpos y puede ser dividida en dos partes, la estática del punto material y la estática del cuerpo rígido.
Punto Material
Para entender la estática del punto material, primeramente precisamos saber de que se trata. Se define como punto material a un objeto cuyas dimensiones no son importantes en el estudio del movimiento. Note que esa definición no está afirmando que para ser un punto material un objeto deba ser obligatoriamente pequeño.
Para entender mejor de que se trata, imaginemos una carretera amplia, donde realizamos un viaje desde Murcia a Valencia. Entonces deseamos estudiar la velocidad media durante este viaje. Esto puede ser realizado de manera bien sencilla, pues solo es necesario realizar la división de la distancia recorrida por el tiempo de viaje, sin que para ello se necesite saber el tamaño de la carretera.
De esta forma podemos considerar la carretera como un punto material, pues el tratamiento de ella en el estudio no es importante.
Estática del Punto Material
Ahora que ya sabemos que es un punto material, debemos pensar en lo que sería necesario para que un objeto con estas características pueda ser mantenido en equilibrio estático. La respuesta se vuelve bastante simple, porque basta con que las fuerzas actuantes sobre el se cancelen, esto es, que la fuerza resultante sea igual a cero.
Para entender mejor el concepto de fuerza resultante, demos
Si quisiéramos profundizar un poco más en este asunto, precisaríams saber sobre el concepto de suma vectorial, pues fuerza es una magnitud vectorial. Existe un método de suma vectorial que es conocido como método poligonal. Tal método está constituído en colocar el origen de un vector en la extremidad del otro formando una “fila” de vectores.
cuando se trata de un punto material en equilibrio, esta “fila” de vectores siempre formará un polígono cerrado, o sea, la extremidad del último vector se encontrará con el origen del primero.
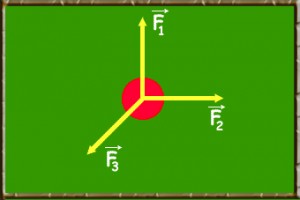
Para aclarar el concepto, consideremos un punto material que está sujeto a tres fuerzas que se cancelan:
Una propiedad de los vectores consiste en el hecho de que nosotros podemos trasladarlos por el espacio sin que sea alterado su sentido, intensidad y dirección.
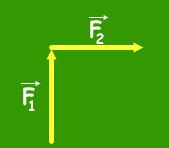
Tomemos inicialmente la fuerza F1, en seguida colocaremos el origen de la fuerza F2, en la extremidad de la F1, y finalmente tomaremos la fuerza F3, y colocaremos su origen en la extremidad de la fuerza F2. El procedimiento descrito está ilustrado en la figura a continuación:
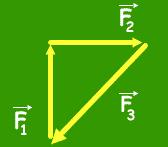
Observemos que logramos formar un polígono cerrado, pues la extremidad de F3, coincidió con el origen de F1. Esto sucede porque las tres fuerzas están anulándose. Caso contrario, existirá un espacio entre el primer y el último vector de la secuencia y con esto, tendríamos una fuerza resultante que apuntaría desde el origen del primero hacia la extremidad del último.
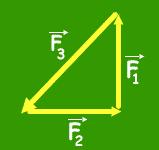
La secuencia elegida en la figura fue F1, en seguida F2 y por último F3, pero ese orden no es obligatorio. Podríamos haber elegido, por ejemplo, F3, luego F2 y por último F1. En este orden o en cualquier otro que fuese permitido, tendremos siempre el mismo resultado final.
Observemos la figura a continuación:
El resultado final para el ejemplo anterior, será cual fuese la secuencia de los vectores será un triángulo rectángulo. Si supiéramos uno de los ángulos de la hipotenusa y por lo menos una de las fuerzas, es posible determinar las otras dos fuerzas trabajando con seno y coseno aplicados al triángulo rectángulo o inclusive, si fuese posible, usar el teorema de Pitágoras.
