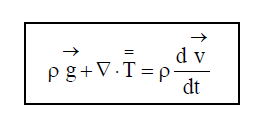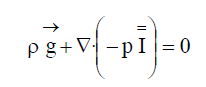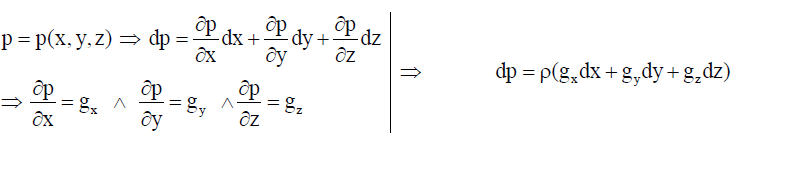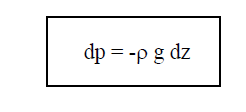Estática de fluidos
En esta ocasión estudiaremos la estática de fluidos, es decir, la parte de la física que trabajo con los fluidos sin movimiento, o más concretamente, estudiaremos cómo se comportan los fluidos cuando no hay movimiento relativo entre sus partículas. Por tanto no puede existir ningún gradiente de sus velocidades. Por tanto no existirá ningún esfuerzo sobre el fluido, y en el caso de que haya alguno tiene que ser normal y a compresión.
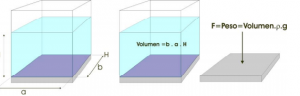
Un ejemplo muy claro de estática de fluidos, es la fuerza que ejerce un fluido cuando está en un recipiente, como el que podemos ver en la imagen, sobre la superficie horizontal. La única fuerza que existe es la del propio peso del fluido.
El concepto más importante de la estática de fluidos es la presión, para su definición nos basaremos en el Principio de Pascal, el cual estableció que la presión es independiente de la dirección.
Definición: La presión de un fluido nos da la fuerza que ejerce el fluido en cada punto de la superficie que lo contiene. Por tanto para calcularla haremos el cociente entre la fuerza y el área: P=F/S. La presión es una magnitud escalar que depende de su posición (x,y,z). La unidad de medida en el sistema internacional (S.I) es el Pascal y en algunas ocasiones la atmósfera.
Observación: Es evidente que la presión variará dependiendo de la profundidad.
ECUACIÓN FUNDAMENTAL DE LA ESTÁTICA DE FLUIDOS
Teniendo en cuanto que si un cuando un fluido está en equilibrio, o lo que es lo mismo, en reposo, también se puede decir que cada una de sus partículas está en equilibrio.
Para dar la ecuación fundamental de la estática de los fluidos, nos basaremos en este caso en la segunda ley de Newton, que en este caso se traduce en que la fuerza resultante (la suma de las fuerzas) tiene que ser nula. Las fuerzas que se ejercen en los fluidos son: fuerzas de volumen, fuerzas de superficie y fuerzas de inercia:
Sumando e igualando a cero, obtenemos la ecuación del equilibrio de fuerzas por unidad de volumen, obteniendo de esta manera la ecuación del movimiento de Cauchy:
Como ya hemos comentado en la introducción del tema, en la estática de fluidos no existen fuerzas inerciales, por la tanto la ecuación anterior se convierte en esta otra:
Si la fórmula anterior la desarrollamos en coordenadas cartesianas, obtenemos la ecuación de equilibrio de fuerzas para un fluido estático:
Para obtener la ecuación fundamental de la estática de fluidos, partimos de la ecuación del movimiento de Cauchy, y obtenemos la ecuación diferencial que nos va a dar la presión en un punto de la superficie a partir de la aceleración y las fuerzas centrales:
Como caso particular del anterior, cuando estamos trabajando en el campo gravitatorio, la ecuación anterior queda de la siguiente manera, obteniendo la ecuación fundamental de fluidoéstatica en el campo gravitatorio: