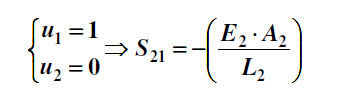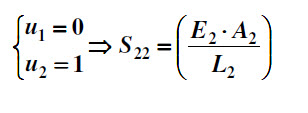Método matricial de la rigidez

Definido el sistema constructivo y el material a ser empleado, el análisis estructural es la primera etapa de un proyecto estructural.

El objetivo del análisis estructural es a partir de una estructura con características geométricas y mecánicas conocidas, sometidas a acciones (cargas o deformaciones impuestas), determinar los desplazamientos (translaciones y/o rotaciones) de todos sus puntos, los esuerzos internos y las reacciones de apoyo.

El análisis estructural es clasificado como lineal, cuando la estructura tiene comportamiento lineal, es no lineal en caso contrario. Para que una estructura tenga comportamiento lineal, ella debe sufrir pequeños desplazamientos y deformaciones específicas y su material debe ser elástico lineal (validad de la ley de Hooke). Esto permite la aplicación del principio de la superposición de los efectos.

Análisis Matricial de Estructuras

El análisis matricial de estructuras es un tópico del análisis estructural en que las ecuaciones que rigen el problema a resolver son formuladas matricialmente, sean ecuaciones de equilibrio de fuerzas o de compatibilidad de deformaciones , dependiendo de método utilizado (método de las fuerzas o método de los desplazamientos), siendo el método de los desplazamientos el más adecuado para la implementación computacional.

El objetivo de esta disciplina es el modelado del análisis estático y lineal de estructuras reticuladas (constituidas por elementos donde una dimensión predomina en relación a las otras dos – barras), utilizado principalmente el método de los desplazamientos con formulación matricial, capacitando a los alumnos a utilizar de forma racional los programas de análisis estructural y a desarrollar sus propios programas.

Fundamentos Teóricos dos Métodos da Flexibilidade e Rigidez

En esta oportunidad veremos los fundamentos teóricos de los métodos de la rigidez y de la flexibilidad. A pesar que estos fundamentos pueden ser aplicables al análisis estructural en general, los veremos específicamente aplicados a estructuras reticuladas, lo que por otra parte cubre un número razonable de elementos estructurales usualmente utilizados en la ingeniería de estructuras.

La formulación de los métodos será desarrollada en álgebra matricial, lo que permite escribir ecuaciones generalizadas para cualquier tipo de estructura con la ventaja adicional de que el abordaje matricial es fácilmente asimilable en algoritmos computacionales, permitiendo el uso de computadoras en el análisis, lo que es la mayor ventaja de estos métodos, desde que el ordenador sea capaz de analizar un gran número de estructuras en tiempo reducido, aumentando considerablemente la productividad del análisis.

Introducción al método de la Rigidez- Abordaje general

La formulación física del método de la rigidez es inversa a la adoptada en el método de la flexibilidad, en tanto, la formulación matemática es idéntica. En el método de flexibilidad las incógnitas a ser calculadas eran las redundantes estáticas, significando que el número de incógnitas a calcular era igual al grado de indeterminación estática.

Ya en el método de la rigidez, las incógnitas a calcularse son los desplazamientos nodales conocidos, significando que el número de incógnitas a calcularse es igual al grado de indeterminación cinemática de la estructura.

Una característica particular del método de la rigidez es el uso intensivo de acciones de extremidad en miembros restringidos que pueden ser obtenidas utilizando el método de la rigidez y luego de colocados en una tabla, aplicados al método de la rigidez.

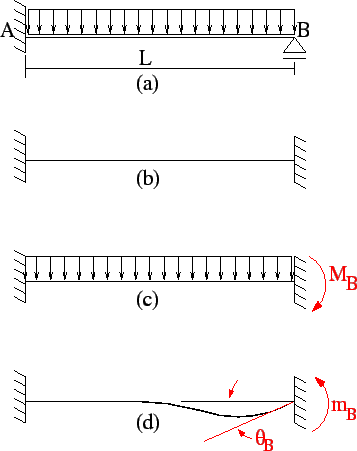
Para ilustrar un abordaje generalizado del método de la rigidez analizaremos la viga cuyo esquema  estructural se presenta a continuación.

Introducción al Método de la Rigidez – Abordaje Matricial

La viga de la figura anterior representa un caso simple de apenas un grado de indeterminación cinemática, didácticamente válido para ilustrar el método de la rigidez, en tanto al analizar una estructura más compleja, con un número mayor de indeterminaciones cinemáticas, es necesario un procedimiento más sistematizado y fácilmente generalizable.

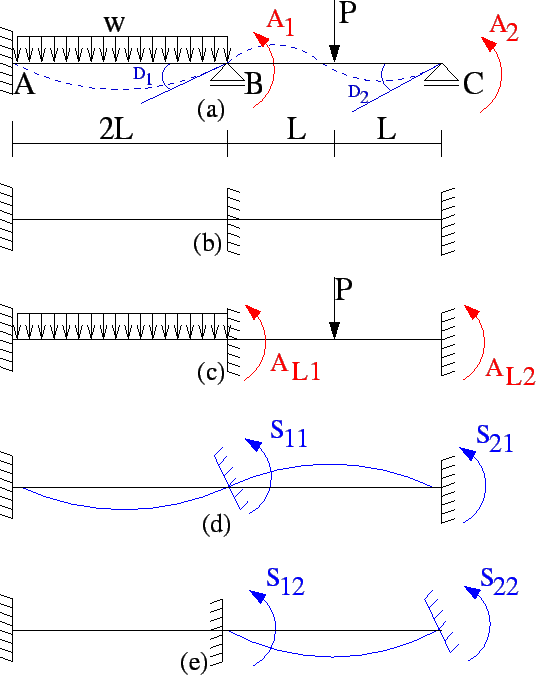
Obtención de la matriz de rigidez de la estructura

La matriz de rigidez de la estructura puede ser obtenida por la conceptualización de sus coeficientes y de las relaciones existentes en la barra sometida a cargamentos axiales.

S₁₁ – es la fuerza en la coordenada 1 resultante de la imposición de un desplazamiento unitario también en la coordenada 1, manteniéndose las demás coordenadas restringidas.

S₂₂ – es la fuerza de la coordenada 2 resultante de la imposición de un desplazamiento en la coordenada 1, manteniéndose las demás coordenadas restringidas.

S₁₂ – es la fuerza en la coordenada 1 resultante de la imposición de un desplazamiento unitario en la coordenada 2, manteniéndose las demás coordenadas restringidas

S₂₂ – es la fuerza en la coordenada 2, resultante de la imposición de un desplazamiento unitario en la coordenada 2, manteniéndose las demás coordenadas restringidas.

Y se obtiene así entonces la matriz de rigidez de la estructura