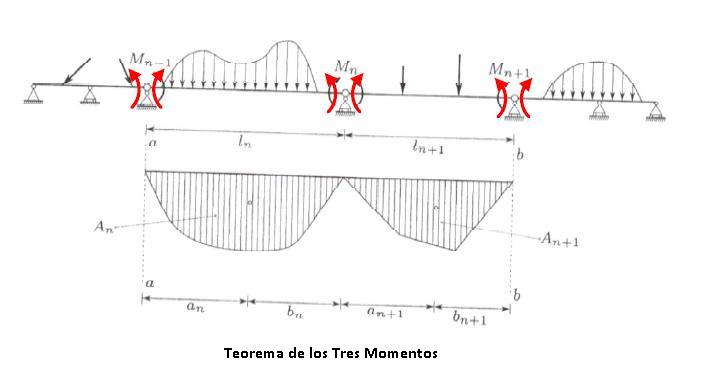
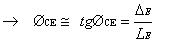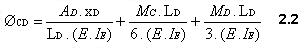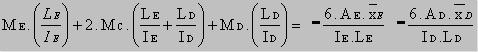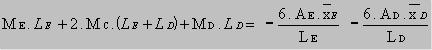Teorema de los tres momentos – Estructuras Hiperestáticas, desplazamientos en flexión
- Aplicables a vigas continuas
- Se calculan los momentos encima de los apoyos
- Las incógnitas Mn pueden ser interpretadas de dos formas:
- Momentos reales encima de los apoyos (los diagramas An serán generados apenas por la carga de los apoyos)
- Momentos hiperestáticos (momentos adicionales en relación a los momentos de la base isoestática; los diagramas son diagramas de esfuerzos de la base isoestática)
Fue desarrollada por los ingenieros franceses Clapeyron y Bertot. Sin perjuicio de que Bertot hubiera publicado primero su artículo, Clapeyron ya había utilizado este método varios años antes para el uso en sus múltiples trabajos con puentes.
El teorema de los tres momentos permite el cálculo de los momentos flectores solicitantes en los apoyos de las vigas continuas. Su deducción está basada en las condiciones de deformación de las vigas en el régimen elástico.
Hipótesis y Limitaciones del teorema de los tres momentos
- Las cargas participantes y las reacciones son todas verticales (perpendiculares al eje de la viga)
- La naturaleza de los apoyos no debe permitir esfuerzos axiales en la viga.
Demostración:
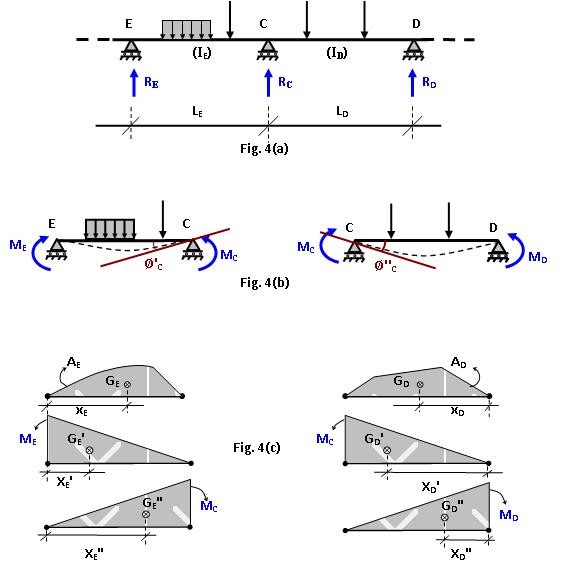
Sea la figura (Fig4a) a continuación:
1º PASO: Creación de la Estructura Primaria
Para este análisis, seleccionamos como redundantes los momentos flectores en las secciones de los apoyos intermediarios de la viga (momentos flectores solicitantes).
A través de la eliminación de los MF en los apoyos (reacciones redundantes), la continuidad de la viga es rota y la estructura primaria así obtenida, consiste en una serie de vigas apoyadas doblemente (Fig4b).
De esta forma cada viga primaria queda sujeta a su cargamento externo y a dos momentos redundantes en sus extremidades (Fig4c)
2º PASO: Igualdad de Deformación Angular para un mismo apoyo
La ecuación necesaria para completar el sistema de ecuaciones de equilibrio estático es obtenida del hecho de que para un mismo apoyo, los tramos adyacentes poseen la misma deformación angular (debido a la continuidad de la LE). Esto nos permite calcular los Momentos Flectores en los diversos apoyos (Fig 5).
En virtud de que la LR es muy aplanada (cepillada, muy lisa) y las flechas ser muy pequeñas se puede admitir que:
Pero de acuerdo con el 2º teorema de los momentos estáticos del área, tenemos:
Entonces:
De forma análoga
De las figuras 5(a) y 5(b), obtenemos que:
Y finalmente cuando procedemos a sustituir 2.1 y 2.2 en 2.3 y actualizamos los términos comunes, se obtiene lo siguiente:
Esta es la ecuación de los tres momentos, pues relaciona tres momentos flectores de apoyos consecutivos en la vida. Ella debe ser descripta para cada apoyo intermedio que esa viga continua que la viga reciba y proveerá tantas ecuaciones cuanto fueren los momentos flectores desconocidos.
La ecuación de los tres momentos se simplifica un poco cuando todos los tramos tienen el mismo momento de inercia “I”