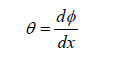Modulo de Torsión
Torsión se refiere al giro de una barra rectilínea cuando es cargada por momentos (o torques) que tienen a producir rotación sobre el eje longitudinal de la barra. Veamos la figura a continuación
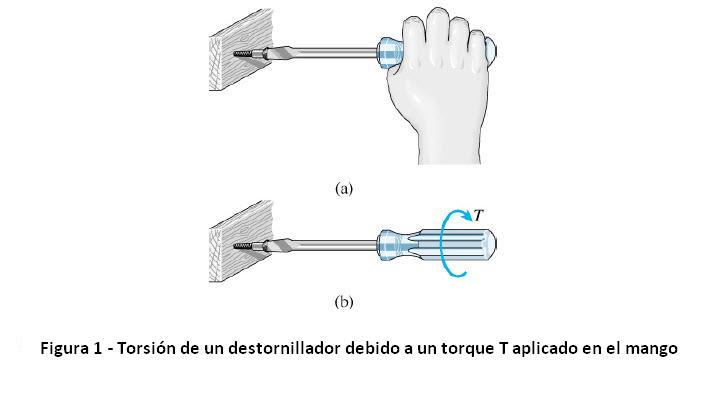
Ejemplos de barras el torsión: Barras, ejes, hélices, ejes de dirección y brocas.
Caso idealizado del cargamento de torsión:
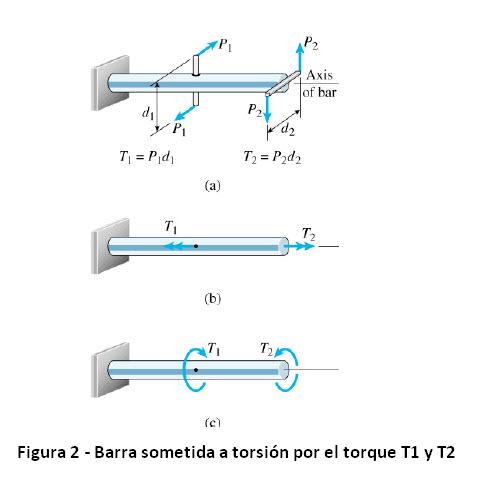
Momentos que producen un giro en la barra como los momentos T1 y T2 de la figura 2, son llamados como torque o momentos de torque.
Miembros cilíndricos sometidos a torques y que transmiten potencia a través de rotación son llamados ejes.
Ejemplo: El cigüeñal de un automóvil o el eje de la hélice de un barco. La mayoría de los ejes tienen secciones transversales circulares, sólidas o tubulares.
Los objetivos del análisis son:
- Desarrollar fórmulas para las deformaciones y tensiones en barras circulares sometidas a torsión.
- Analizar el estado de tensión conocido como corte puro y obtener la relación entre los módulos de elasticidad E y G en tracción y corte respectivamente.
- Análisis de ejes de rotación y determinación de la potencia que ellos transmiten
Deformación de torsión de una barra circular
Consideremos una barra prismática de sección transversal circular girada por torques T actuando en las extremidades como en el Figura 3.
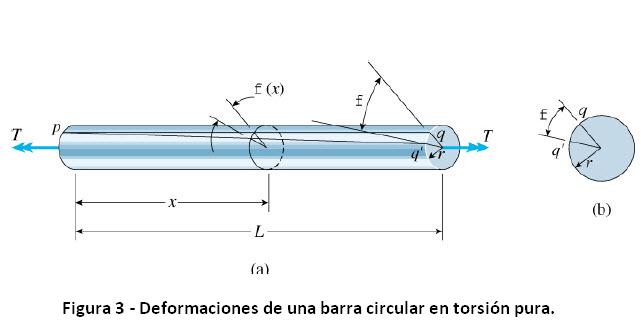
Torsión Pura: Toda la sección transversal está sometida al mismo torque interno T.
Consideraciones:
De las condiciones de simetría las secciones transversales de la barra no varían en la forma en tanto rotan sobre el eje longitudinal. En otras palabras todas las secciones transversales permanecen planes y circulares y todos los rayos permanecen rectos.
Caso el ángulo de rotación entre una extremidad de la barra y otra es pequeño, ni el largo de la barra y ni su radio irán a variar.
Variables:
f, φ – Ángulo de Torsión
El ángulo de torsión varía a lo largo del eje de la barra: 0 ≤ φ(x)≤ φ
Si toda la sección transversal de la barra tiene el mismo radio y está sometida al mismo torque (torsión pura), el ángulo φ(x) variará linealmente.
Consideremos la figura 4
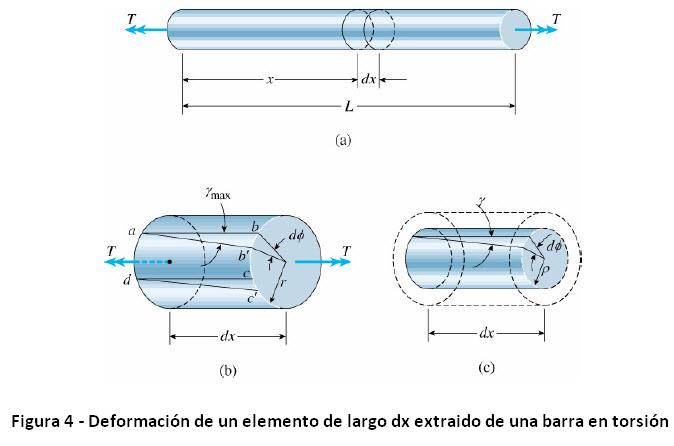
Los ángulos en la esquina del elemento en la figura 4b no son ya iguales a 90º. El elemento está en un estado de corte puro y la magnitud de la deformación de corte gmax es igual a la disminución en el ángulo en el punto a, esto es, la disminución en el ángulo bad. De la figura vemos que la disminución de este ángulo es:
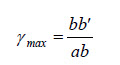
Donde gmax se mide en radianes, bb’ es la distancia a través de la cual el punto b se mueve y ab es el largo del elemento (igual a dx). Con r denotando el radio de la barra, podemos expresar la distancia bb’ como rdφ, en que dφ también se mide en radianes. De esta forma la ecuación anterior quedará:
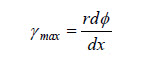
Esta ecuación relaciona la deformación de corte en la superficie externa de la barra con el ángulo de torsión.
La relación dφ/dx es la razón de la variación del ángulo de torsión φ en relación a la distancia x medida a lo largo del eje de la barra. Vamos a denotar dφ/dx por el ángulo θ y nos referimos a él como razón de torsión o ángulo de torsión por unidad de medida.