Centro de oscilación

Se dice que el péndulo es una reversible que se suspende en otro punto y muestra la frecuencia de oscilación misma.

Tendrás la oportunidad de estudiar el movimiento de un péndulo reversible mediante un programa simulador. Este programa reproduce el movimiento característico del péndulo, basado en un modelo matemático, que ofrece la posibilidad de interacción con el usuario que actúa como una herramienta de «experiencia virtual». El programa dibuja el gráfico de los puntos obtenidos por medio del experimento virtual, dando la posibilidad de que se están elaborando las conclusiones sin necesidad de cálculos adicionales que tienen lugar.

Se propone una solución teórica al problema que implica el péndulo reversible, que puede ser comparada con la respuesta «experimental». La solución teórica se resuelve mediante el cálculo algebraico, Arce con el programa, y tampoco son necesarios los cálculos de lápiz y papel.

La física del péndulo compuesto

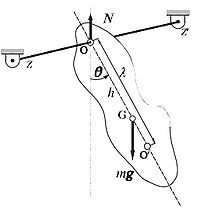
Un péndulo compuesto puede girar libremente alrededor de un eje que pasa por el punto P. En la posición de equilibrio (q = 0) el centro de masa C está alineado con el punto P, situado justo debajo de este. La distancia entre P y C es a. Supongamos, además, que el cuerpo tiene un momento de inercia para el punto de oscilación P.

Para hacer un análisis del movimiento del cuerpo cuando se libera, debemos considerar que su masa se encuentra en el centro de la masa de C, en los que opera bajo el peso, produciendo un par de camisolas con el punto P. Este par es la única causa del movimiento del cuerpo.

Cuando el cuerpo se desplaza de su posición de equilibrio según el ángulo q se somete a una torsión de la fuerza del peso actúa en su centro de masa, dado por la expresión

t = – g pecado M (q)

A medida que el par actúa siempre a fin de restablecer la condición de equilibrio conduce al punto C la vertical de P el lado derecho de la ecuación y tiene un signo negativo (q es positivo cuando el par es negativo y viceversa). M es la masa el cuerpo y g es la aceleración de la ubicación de la gravedad. Para pequeñas oscilaciones, cuando q es inferior a 20 grados, podemos usar la aproximación:

sen (q) q ~

y la ecuación 1 será:

t = – g q M

Pero este esfuerzo de torsión también se puede calcular mediante la ecuación:

t = I a = I d 2 q / dt 2

Donde I es el momento de inercia del cuerpo hasta el punto P y el es la aceleración angular del péndulo.

Igualando las ecuaciones:

d 2 q / dt 2 + Mga q / I = 0

¿Cuál es la característica de la ecuación diferencial del movimiento armónico simple, y tiene una posible solución del tipo:

q = q 0 cos (w t + d)

Donde w es la siguiente:

w = (MGA / I) 1 / 2

Y el período de oscilación:

T = 2 p (E / Mga) 1 / 2

Al igualar la ecuación para el período de la ecuación del péndulo para el período que consiste en un péndulo simple, es la longitud l 0 del péndulo simple equivalente del péndulo compuesto. Por lo tanto:

2 p (0 l / g) 1 / 2 p = 2 (I / mga) 1 / 2

l 0 = E / Ma