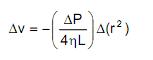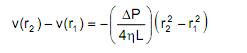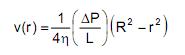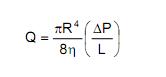Ley de Poiseuille

Vamos  a considerar el movimiento de un fluido a través de un tubo cilíndrico en un referencial fijo en el tubo. Cuando todos los elementos de volumen del fluido que pasan por un punto cualquiera dentro del tubo lo hacen siempre con la misma velocidad, el flujo se llama fijo o permanente

En puntos diferentes, las velocidades de los elementos de volumen pueden ser diferentes. Un flujo estacionario puede ser logrado si el fluido se traslada con velocidad de módulo relativamente pequeño.

Consideremos entonces un fluido viscoso en un flujo estacionario y laminar a través de un tubo cilíndrico. De esa forma, el fluido se divide en capas cilíndricas coaxiales, que se mueven  con velocidades de módulos diferentes.

La capa mas externa, llamada como capa límite, adhiere a la pared del tubo y tiene velocidad nula en el referencial considerado

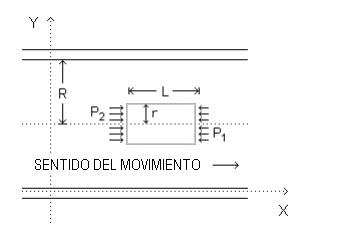
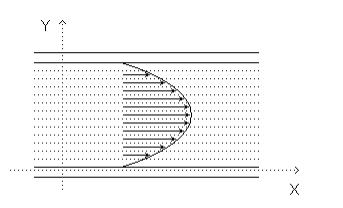
La capa central tiene velocidad de módulo máximo. Para discutir el valor del módulo de la velocidad e cada capa en función de su distancia al eje de un tubo cilíndrico de radio R, consideremos un elemento cilíndrico de radio R, consideremos un elemento cilíndrico del fluido de radio r y largo L, coaxial con el tubo (Figura a continuación)

 

El elemento cilíndrico escurre por efecto de una diferencia de presión:

De forma que la fuerza que lo impulsa en el sentido de su movimiento tiene módulo:

Esta fuerza debe estar en equilibrio con la fuerza de viscosidad que actúa en sentido contrario, en la superficie cilíndrica del elemento de fluido considerado, Como el área de esa superficie es Δ = 2πrL , podemos escribir:

Y como:

Entonces tenemos:

O entonces de forma más detallada:

 

Si esta expresión es aplicada entre una capa cilíndrica genérica cualquiera, de radio r1 = r, que se desplaza con velocidad de módulo v y la capa límite, que se encuentra en contacto con la pared del tubo de radio r2 = R que se encuentra en reposo obtenemos:

Esta expresión muestra que el módulo de la velocidad de una dada capa cilíndrica del luido en un referencial fijo en el tubo es directamente proporcional al gradiente de presión ΔP/L e inversamente proporcional al coeficiente de viscosidad η.

Además de esto, la capa cuya velocidad tiene el módulo máximo es la capa central para la cual r = 0 y la capa cuya velocidad tiene el módulo mínimo (es igual a cero) es la capa límite para la cual r = R.

Entre esos dos extremos, la variación es parabólica (figura anterior)

La velocidad de flujo, es decir, el volumen de fluido que pasa a través de una sección transversal del tubo por unidad de tiempo está dada por la ecuación de Poiseuille:

Por tanto la velocidad del flujo es directamente proporcional al gradiente de presión sobre el fluido e inversamente proporcional a la viscosidad como es de esperar.

Por otra parte, escribiendo:

Podemos interpretar la constante entre paréntesis como una especie de resistencia al escurrimiento

Así, esta expresión guarda cierta analogía con la expresión: ΔV = Ri que representa la diferencia de potencial eléctrico en un resistor de resistencia R, recorrido por una corriente i.