Aceleración circular uniforme ó aceleración centrípeta
Newton propuso lo que llamamos hoy ley de gravitación de Newton, o ley de gravitación universal, donde toda partícula atrae a otra con una fuerza gravitacional.
Ley de la gravitación para órbitas circulares:
De acuerdo con la segunda ley de Newton, el movimiento es uniforme para una órbita circular. La aceleración en este caso es centrípeta, cuya velocidad angular está dada por la ecuación w = 2p /T en una cierta órbita circular de radio R. Donde r es el vector unitario en la dirección radial.
Si m es la masa del planeta, entonces la fuerza que actúa sobre el está dada por la segunda Ley de Newton:
Por la tercera ley de Kepler tenemos:
Donde C tiene igual valor para todos los planetas. Entonces:
Basándose en la ley de los períodos de Kepler, Newton concluyó que la fuerza gravitacional varía inversamente con el cuadrado de la distancia del planeta al Sol. Por la tercera Ley de Newton, el planeta ejerce una fuerza igual y contraria sobre el sol, la cual debe ser proporcional a la masa M del Sol. Newton por su parte fue llevado a la conclusión matemática anterior.
Donde G sería ahora una constante universarl característica de la fuerza gravitacional. Esta es, por tanto la Ley de Newton de la gravitación. La ley Universal de gravitación de Newton puede ser enunciada de la siguiente forma:
“Cada partícula del universo atrae cada una de las otras partículas con fuerzas directamente proporcionales al producto de su masa e inversamente proporcional al cuadrado de la distancia que separa esas partículas. La dirección que tiene esta fuerza, es la de la línea que une las partículas”
Newton procuró comparar la fuerza necesaria para mantener la Luna en su órbita con la fuerza de gravedad en la superficie de la Tierra.
Adoptando la siguiente notación: T=Tierra; L=Luna; M= manzana de un árbol
Por tanto, los módulos de las fuerzas mencionadas serán:
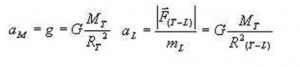
Sean aL y aM los módulos de las aceleraciones de la Luna y de la manzana; esta última es igual a g (gravedad). Además de esto R (T-M) =RT (radio de la Tierra)
Entonces:
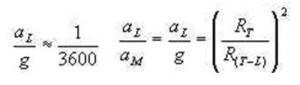
Para realizar la verificación era necesario el valor de RT y R (T-L). Hiparco (en el añ 130 a.C.) había concluido que la distancia de la Tierra a la Luna es 59 veces el radio de la Tierra a través de sus cálculos. Newton utilizó 60 como el valor adecuado y obtuvo entonces:
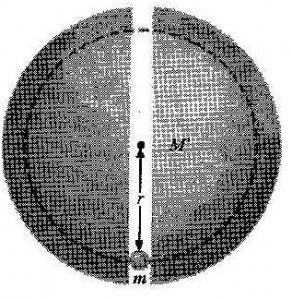
Lo que concuerda con el valor calculado de la aceleración centrípeta de la Luna
Con esto, Newton brindó la contribución básica para la física mostrando que la fuerza que mantiene la Luna en su órbita es la misma que logra que la manzana caiga al suelo desde el árbol.
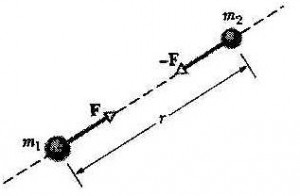
Pero para ello, Newton tuvo que considerar la Tierra como una cáscara esférica y con toda su masa concentrada dentro del núcleo. Así, desde el punto de vista de la manzana, la Tierra se comporta como una partícula localizada en su centro y teniendo su masa (como muestra la figura a continuación).
Newton no solo concluyó que la Tierra atrae la manzana y también la Luna, sino que cualquier cuerpo del universo atrae todos los demás. Dos manzanas por ejemplo, son atraídas una por la otra a una distancia de 20 cm entre ellas. Sin embargo, existe una atracción mayor que es la de las manzanas por la Tierra, esta atracción es tan grande que inhibe los efectos de atracción entre las dos manzanas.
La manzana atrae a la Tierra con la misma intensidad que la Tierra atrae la manzana. Sin embargo, sus aceleraciones son diferentes. La aceleración de una manzana cayendo es de 9,8 m/s2 (aceleración de la gravedad de la superficie de la Tierra). Ya, una bola de boliche de masa 7,0 Kg, sufre una aceleración de 1,2×10-23 m/s2 (como podemos verlo en la figura anterior).
