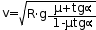La fuerza centrífuga (y centrípeta)
En la dinámica de los movimientos circulares hemos visto que cuando un objeto describe un movimiento circular sobre él ha de actuar una fuerza centrípeta que le obligue a describir la curva. Ésta venía dada por la aceleración normal a la trayectoria de la curva, que era constante en el caso de un movimiento circular uniforme (MCU) y variable en el caso de un movimiento circular uniformemente acelerado (MCUA). De no ser así, como consecuencia del principio de inercia, continuaría moviéndose en la dirección de la velocidad y de la aceleración tangente, es decir, en línea recta. Según el principio de acción y reacción, donde toda fuerza tiene una opuesta porque funcionan a pares, se deduce que el objeto ejercerá otra fuerza igual y contraria sobre quien le aplica la fuerza centrípeta. A esta fuerza la denominamos fuerza centrífuga y tiene el mismo valor que su pareja y el sentido opuesto, es decir, radial hacia afuera.
¿A que si haces girar una piedra atada a un hilo muy rápidamente sientes como tu mano se ve atraída por la piedra al final del hilo?
Y si observas a un atleta lanzador de martillo verás cómo echa su cuerpo hacia atrás cuando lo voltea. De este modo evita caerse al suelo debido a la fuerza centrífuga que actúa sobre él.
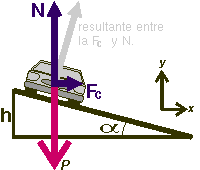Así, cuando un vehículo toma una curva, podemos imaginar que sobre él actúan dos fuerzas: su peso y la fuerza centrífuga, dando una resultante que será más inclinida cuanto cuanto mayor sea la velocidad del vehículo y menor el radio de la curva. Ese es el efecto que sentimos al viajar en coche cuando tomamos una curva muy rápido y sentimos que el lateral del coche en el exterior del giro se eleva un poco. Para evitar que el vehículo patine o vuelque es necesario que esa fuerza resultante no se salga de la base de sustentación y que, a ser posible, sea perpendicular a la carretera para que sea anulada por la reacción del apoyo del vehículo sobre el suelo.
En realidad, la explicación es otra e implica a las fuerzas de rozamiento. Si la carretera está sin peraltar (elevada de un lado), la fuerza centrípeta es originada por el rozamiento lateral de las ruedas contra el suelo: Fr=µ·m·g=(mv2)/r de donde: r=v2/(µ·g) (1). Si la carretera está peraltada un cierto ángulo φ y no existe rozamiento, la tangente del ángulo de peralte viene dad por la relación fuerza centrípeta/peso del vehículo:
tgφ=[(m·v2)/r]/m·g=v2/(r·g) , de donde: r=v2/(g·tgφ) (2).
Si, como sucede normalmente, la carretera está peraltada y existe rozamiento, el cálculo del radio de la curva es más complejo. Viene dado por la expresión: r=[v2(1-µ·tgφ)] / [g·(µ+tgφ)]. Fórmula de la cual se deducen las dos anteriores. En la primera φ=0 y la segunda µ=0.
Ahora voy a proponer un ejercicio modelo resuelto:
Supongamos que un vehículo de masa m se dispone a tomar una curva de radio R. Calcula la velocidad máxima con que puede tomar la curva sin deslizar en las siguientes situaciones:
a) La curva no está peraltada y no hay rozamientos.
No existe agente que suministre la fuerza centrípeta. El vehículo no podrá girar.
b)Si no hay peralte, pero sí rozamientos (µ).
Los rozamientos proporcionarán la fuerza centrípeta.
Fr=µ·N y N=P=m·g, por lo tanto Fr=µ·m·g —> Éste será el valor máximo que puede tomar la fuerza centrípeta. Así pues, (m·v2)/R=µ·m·g —>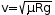 
c)La curva está peraltada y se desprecian los rozamientos.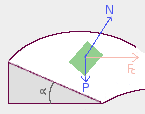
Al estar peraltada se consigue que parte del peso suministre la fuerza centrípeta.
tgα=Fc/P –> Fc=P·tgα=m·g·tgα. Por lo tanto (m·v2)/R=µmg –>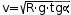
d)La curva está peraltada y µ es el coeficiente de rozamiento.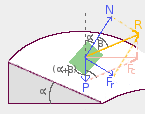
Fr hacia abajo porque se opone a que se salga de la curva, R es la resultante entre N y Fr y Fc es la resultante entre R y P. tg(α+β)=Fc/P —> Fc=P·tg(α+β). La tg(α+β)=(tgα+tgβ)/(1-tgαtgbeta;) y como la tgβ=Fr/N=µ. Por lo tanto, tg(α+β)=(µ+tgα)/(1-µtgα) y así la fuerza Fc=mg·(µ+tgα)/(1-µtgα)=(mv2)/R. Despejando v obtenemos una velocidad: 
