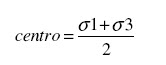Mecánica de Suelos – Ruptura de Suelos
Ciertos deslizamientos de pendientes naturales están vinculados al comportamiento característico de arcillas que poseen una resistencia final, a largo plazo, muy baja, al mismo tiempo que exhiben viscosidad elevada.
Por ello presentan resistencias a corto plazo muy elevadas, permitiendo inclusive cortes verticales de algunas decenas de metros, pero sólo adquieren un perfil de estabilidad razonable a lo largo del tiempo.
Para varios materiales utilizados en ingeniería han sido propuestos «criterios de ruptura», que demuestran en términos de tensión o extensión los parámetros que condicionan la ruptura del material.
El criterio de Rankine expresa que la ruptura está condicionada por la máxima tensión principal. El criterio de St. Venant dice que la ruptura está determinada por la máxima extensión principal. El criterio de Tresca atribuye la ruptura a la máxima tensión tangencial. El criterio de Mohr-Coulomb dice que la ruptura se da cuando en una familia de facetas de la tensión alcanza una inclinación crítica (f), con la normal a la faceta.
La ruptura será cuando la tensión tangencial alcanza el valor sn.tgf, de forma que:
Para arcillas saturadas son expuestas a requisitos rápidos y para arcilla de cohesión muy elevada, el criterio de Tresca se ajusta mejor a la descripción de los fenómenos de ruptura.
La representación geométrica determinada por «círculo de Mohr” es una cómoda representación del estado de tensión en un punto.
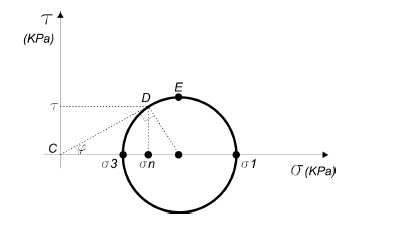
Figura – Círculo de Möhr representativo de estado de tensión en un punto
Donde:
s3 – tensión principal mínima
s1 – tensión principal máxima
En el punto D incide una tensión total (s), con componente normal (sn), y componente tangencial (t). La tensión total hace un ángulo f, con la faceta representada por D.
El punto E representa la faceta en que es máxima la tensión tangencial.
Teniendo un suelo en el cual se va incrementando carga a sus tensiones principales en un punto dado en el interior del macizo, van aumentando hasta alcanzar la tensión de ruptura, valoren el cual el material entra en ruptura.
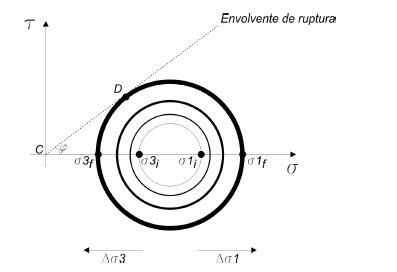
Figura – Comportamiento de un suelo con aumento incremental de carga
a medida que se incrementa la carga, los círculos de Möhr van aumentando y por tanto s1 y s3 van también aumentando.
Cuando se alcanza el círculo que es tangencial a la línea CD el material entra en ruptura.
Los materiales térreos exhiben resistencias residuales elevadas. O sea la resistencia ofrecida por el material a la deformación inclusive después de alcanzada la ruptura es satisfactoria.
Y así es que los suelos tienen rupturas no frágiles con apreciable resistencia residual.
1) Criterio de ruptura de Möhr-Coulomb: el material entra en ruptura cuando la relación entre las dos tensiones, adquiere una determinada inclinación. Este criterio se aplica a materiales donde existe rozamiento. Si no existe el rozamiento no se utiliza criterio.
2) Ángulo de rozamiento: Máximo ángulo de la tensión puede hacer con la normal a la faceta.
Figura – Criterio de ruptura de Möhr-Coulomb
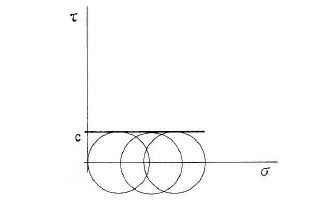
3) Criterio de ruptura de Tresca: la ruptura será cuando en un conjunto de facetas se da un determinado valor de tensión tangencial. La envolvente de Möhr – Coulomb es ahora paralela al eje de tensión normal (σ). En estas situaciones el rozamiento es nulo.
Figura – Criterio de ruptura de Tresca
Diferencias y principales diferencias entre los criterios de ruptura de Möhr – Coulomb y de Tresca
El criterio de ruptura de Möhr-Coulomb dice que un material entra en ruptura en un punto, cuando en una faceta pasando por ese punto, la tensión alcanza una determinada oblicuidad en relación a la normal respectiva.
No es la magnitud de tensión que determina la ruptura, pero si su oblicuidad. La ruptura se obtiene por haberse alcanzado cierta relación entre el componente tangencial y el componente normal de tensión.
Esta teoría se refiere más a materiales cuya resistencia es esencialmente debida a fenómenos de rozamiento que desarrollan en su interior.
El criterio de ruptura de Tresca postula que un material entra en ruptura en un punto pasando una faceta conjunto de facetas pasando por ese punto, se alcanza un valor dado de la tensión tangencial. En este caso ya no es la magnitud de uno de los componentes de tensión que ocasiona la ruptura. Un material que obedezca a este criterio de ruptura es puramente cohesivo y no posee rozamiento interno.
Las arenas suelo granulares obedecen bien a la condición de Möhr-Coulomb, con cohesión nula. Las arcilla pueden obedecer consonante a las condiciones en que es aplicado el requisito por corte, la condición de Tresca p de Möhr-Coulomb (con cohesión nula).