Fundamentos de Óptica geométrica (I)
Rayo de luz
Las trayectorias de la energía radiante en su propagación constituyen los rayos de luz.
Si un punto de emisor O, lo ponemos delante de una pantalla con un orificio, el punto y el orificio definen un cono lleno de luz que recibe el nombre de haz. Si las dimensiones del orificio son pequeñas, el cono se llama pincel. Si hacemos que el diámetro del orificio tienda a cero, llegamos a una abstracción del haz sin realidad física; esta abstracción ideal constituye el rayo de luz.
Índice de refracción
La luz se propaga en el vacío con una velocidad constante c=299792,5 km/s
En un medio material la velocidad de la luz disminuye y su valor depende de la constitución del medio.
Desde el punto de vista óptico podemos caracterizar a los medios materiales por un escalar n que es el índice de refracción.
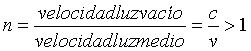
Como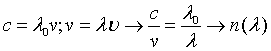 
La dependencia de n provoca un fenómeno conocido como “dispersión cromática”. El único medio no dispersivo es el vacío n=1.
Clasificación de los medios materiales
Atendiendo al índice de refracción:
• Homogéneos e isótropos: el índice de refracción es cnte en todos los puntos y en todas las direcciones. Por ejemplo vidrios ópticos.
• Anisótropos: el índice de refracción varía punto a punto. Por ejemplo la atmósfera.
• Inhomogéneos y anisótropos: el índice de refracción varía punto a punto y con la dirección.
Camino óptico. Principio de Fermat
Si en un medio homogéneo e isótropo (n=cnte) la luz recorre un trayecto de longitud d, el camino óptico L, conocido también como función eikonal, se define como L=nd
“Camino óptico es el camino geométrico que recorre la luz en el medio multiplicado por el índice de refracción”
Representa también la distancia que recorrería la luz en el vacío en el tiempo que invierte en recorrer el camino geométrico d
Si el trayecto es a través de diferentes medios de índices, recorriendo en ellos distintas longitudes, el camino óptico es aditivo y vendrá dado por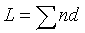 
Para el caso general, dada una curva C que representa la trayectoria de un rayo de luz, se denomina camino óptico entre dos puntos A y B de dicha curva a la integral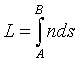 
. Si el medio es homogéneo e isótropo L=nd siendo d la distancia entre los puntos A y B.
La óptica geométrica se puede construir tomando como axiomas la propagación rectilínea de la luz en medios homogéneos e isótropos y las leyes de Descartes (leyes de reflexión, refracción y conservación del plano de incidencia mas la no interacción de los rayos luminosos). Pero es más efectivo partir de un único postulado de un principio variacional(principio de Fermat) del cual se obtienen como teoremas las leyes anteriores. Así pues llegamos al principio de Fermat, el cuál veremos en el próximo post.
Reflexión y Refracción de la Luz
La reflexión y la refracción son fenómenos fundamentales en la óptica geométrica. La reflexión ocurre cuando un rayo de luz incide sobre una superficie y se refleja, obedeciendo la ley de reflexión que establece que el ángulo de incidencia es igual al ángulo de reflexión. Este fenómeno es evidente en superficies como espejos.
La refracción, por otro lado, se produce cuando un rayo de luz pasa de un medio a otro con diferente índice de refracción, cambiando su velocidad y dirección. La ley de Snell describe este comportamiento mediante la relación:
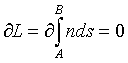
donde θ1 y θ2 son los ángulos de incidencia y refracción, respectivamente, y n1 y n2 son los índices de refracción de los medios. Este fenómeno es responsable de efectos como la desviación de la luz al pasar del aire al agua, creando ilusiones ópticas como el aparente doblamiento de un objeto sumergido.
Aplicaciones de la Óptica Geométrica
La óptica geométrica tiene numerosas aplicaciones prácticas en la vida cotidiana y en la tecnología. Por ejemplo, en la fabricación de lentes para gafas y cámaras, donde se utilizan principios de refracción para corregir la visión o enfocar imágenes. Los telescopios y microscopios también se basan en estos principios para ampliar objetos distantes o pequeños.
Además, la fibra óptica, que es esencial para las telecomunicaciones modernas, utiliza la reflexión interna total para transmitir señales de luz a largas distancias con mínima pérdida de información. Este avance ha revolucionado la transmisión de datos, permitiendo conexiones de internet de alta velocidad y comunicaciones globales eficientes.
En la medicina, la óptica geométrica es crucial en técnicas como la endoscopia, donde se utilizan fibras ópticas para visualizar el interior del cuerpo humano sin necesidad de cirugía invasiva. También se emplea en la corrección de la visión mediante la cirugía láser, donde se moldean las córneas para mejorar la refracción de la luz en el ojo.
La comprensión de estos principios no solo es fundamental para la física, sino que también impulsa innovaciones tecnológicas que mejoran nuestra calidad de vida y expanden nuestras capacidades científicas.