Fundamentos de Óptica geométrica (II)

-Principio de Fermat

“La trayectoria real (rayo) que sigue la luz para viajar desde el punto A hasta el punto B es aquella para la cual el camino óptico L entre ambos puntos es estacionario, es decir ”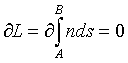

El camino óptico entre 2 puntos a lo largo de un rayo puede ser, por tanto, máximo, mínimo o mantenerse constante con respecto a trayectorias próximas a él.

Podemos ver la similitud entre el Principio de Fermat y el Principio de Hamilton de la mecánica clásica.

A partir del principio de Fermat, puede definirse un rayo luminoso como aquella curva que hace estacionario el camino óptico entre dos puntos. Asimismo, el Principio de Fermat, trae otra consecuencia fundamental: la reversibilidad de los rayos de luz.

Si la luz puede viajar a lo largo de un rayo desde el punto A hasta el punto B también podrá hacerlo siguiendo la misma trayectoria pero en sentido contrario, desde B hasta A. En otras palabras, la condición estacionaria es independiente del sentido de recorrido a lo largo del rayo que une los dos puntos.

Si resolvemos la ecuación de trayectoria de rayos (Principio de Fermat) obtenemos que en un medio homogéneo los rayos luminosos tienen la forma de líneas rectas, es decir describen trayectorias rectilíneas.

-Leyes de la óptica geométrica

1) Ley de la reflexión

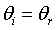
Podemos obtener esta ley a partir del principio de Fermat, cosa que aquí no demostraré.

2) Ley de la refracción

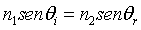
El valor límite o crítico del ángulo de incidencia para obtener rayo refractado será

Superficies de onda y teorema de Malus-Dupin

“Si tenemos una fuente puntual, en un medio cuyos rayos salen en todas las direcciones y sobre estos rayos se toman caminos ópticos iguales desde la fuente, los puntos extremos de tales recorridos se encuentran sobre una superficie perpendicular a estos rayos” Esta superficie se llama superficie de onda (también conocida como frente de onda geométrico). Éste es el enunciado del Teorema de Malus-Dupin.

El camino de óptico entre frentes de onda geométricos, calculado a lo largo de cualquier rayo que conecte ambos frentes, es el mismo.

Se puede generalizar al frente de onda geométrico que ha sufrido un número cualquiera de refracciones y/o reflexiones por superficies.

Los rayos luminosos son trayectorias ortogonales a los frente de onda para los cuales L=cnte.