Teoría de la relatividad restringida o especial

En el artículo anterior describimos cómo se descubrió que la existencia de una materia hipotética llamada éter, que se suponía ocupaba todo el espacio vacío para poder explicar la propagación de la luz, era en realidad una mala idea. Los experimentos de Michelson y Morley lo demostraron.
Ahora, veamos la interpretación que dio Einstein de todo esto.
En 1906 Einstein publica «Sobre la electrodinámica de los cuerpos en movimiento«. Su Teoría de la Relatividad Restringida se basa en dos postulados fundamentales:
«Las leyes físicas son idénticas en todos los sistemas inerciales y se expresan mediante ecuaciones análogas» y
«La velocidad de la luz en el vacío es constante y la máxima posible en nuestro Universo; siendo independiente del movimiento del foco luminoso o del observador«.
La primera se refiere a que no existe un movimiento absoluto, sino que el movimiento de un sistema siempre viene definido respecto a otro. La segunda es una generalización de la conclusión del experimento de Michelson-Morley.
Las consecuencias de esta nueva teoría dan un nuevo sentido al espacio, la masa, la energía y el momento lineal. Analicemos una a una:
Longitud:
FitzGerald y Lorentz, a partir de los experimentos de Michelson y Morley dedujeron de forma teórica (luego la teoría de Enstein se encargó de demostrar) que aunque los brazos del interferómetro era realmente iguales en longitud, se comportaban como si no fuera así. Propusieron que el brazo situado en la dirección del movimiento se contraía, con lo que, al igualarse los caminos ópticos de los dos haces de rayos, se igualarían también los tiempos invertidos en sus recorridos.
Se enuncia pues:
Todos los cuerpo materiales que se muevan a través del éter se contraen en la dirección de su movimiento en una proporción √(1-(v2/c2)) sin que sufran modificación alguna sus dimensiones transversales.
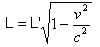
donde L» representa la longitud real medida por un observador en reposo.
Tiempo:
Dos sucesos que son simultáneos en un sistema de referencia no lo serán si se observan desde otro sistema de referencia en movimiento respecto al primero.
Esto quiere decir que el tiempo, en contra de lo que Newton decía, no es absoluto sino que, al igual que ocurre con el movimiento, depende del sistema de referencia y por lo tanto que dos sucesos seaN simultáneos es relativo al movimiento del propio observador.
Einstein va más allá y afirma que el tiempo se dilata, es decir, que es mayor, cuando los dos ducesos ocurren en un sistema inercial en lugar de en un sistema en reposo.
El tiempo se dilata cuando el cuerpo está en movimiento. Los relojes móviles parecen avanzar más lentamente (retrasar) que los fijos.
En este caso, la diferencia de tiempo entre dos sucesos que ocurren en un sistema en movimiento es:
Para concluir con el tiempo definiremos que: «La simultaneidad sólo es absoluta cuando dos sucesos ocurren en el mismo lugar y al mismo tiempo«.
Velocidad:
La antigua ley de la mecánica clásica que decía que si un móvil lleva una velocidad y éste es arrastrado, su velocidad total es la suma (u=u»+v) se sustituye por esta otra:
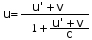
para asegurar que ninguna suma de velocidades supera la velocidad de la luz (c). Para comprobarlo, sustituye, u»=c y verás que u=c.
Por lo tanto el teorema es:
La velocidad de la luz en el vacío es una velocidad límite y no es posible superarla.
Masa:
Kauffmann, ya en 1902, sospechó que la masa de los electrones aumentaba con la velocidad de éstos.
Einstein probó que la masa realmente depende de la masa en reposo (m0) y la velocidad:
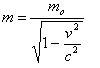
Energía:
Como sabemos: F=δp/δt y el trabajo es δW=F·δs. Por lo tanto: δW=δp/δt·δs=v·δp.
De la expresión relativista de la masa, arriba, se deduce que (p=m·v): p=c·√(m2-m02) por lo tanto, δp=c·(m·δm)/√(m2-m02).
Multiplicando numerador y denominador por c y operando queda: δp=c2/·δm y sustituyendo en la expresión del trabajo: δW= c2·δm = δE.
Por lo tanto, referido a una variación de masa Δm:
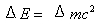
A toda variación de masa le corresponde una variación de energía, cumpliéndose que la relación ΔE/Δm es constante e igual al cuadrado de la velocidad de la luz en el vacío.
