Ecuaciones de estado(I)

-Ecuaciones de estado energética y térmicas de un sistema

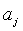La formulación del segundo postulado o principio cero de la termodinámica pone de manifiesto el hecho de que el estado termodinámico de un sistema queda determinado, no solamente por sus parámetros externos, sino también por la tª. Ésto significa que los parámetros internos , de un sistema en equilibrio termodinámico son funciones de los parámetros externos y de la temperatura T o tita , es decir, 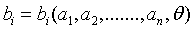i=1,2,….. (1)

Expresión que constituye la formulación matemática del segundo postulado de la termodinámica.

Por definición, las n ecuaciones (1) para las cuales el parámetro interno coincide con la fuerza generalizada A , asociada al parámetro externo 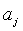, reciben el nombre de ecuaciones térmicas de estado del sistema en cuestión. Matemáticamente se expresan así: 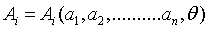i=1,2,…. (2)

Asimismo, aquella ecuación de entre las (1) para la cual el parámetro interno considerado sea precisamente la energía del sistema, U, recibe el nombre de ecuación energética de estado: 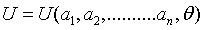(3)

Obviamente, para un sistema simple, las n+1 ecuaciones (2) y (3) se reducen solamente a dos: 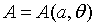y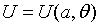

En cualquier caso, la forma analítica de las ecuaciones energética y térmica de estado depende del sistema considerado y su deducción puede realizarse, bien por vía experimental, bien por vía teórica , utilizando métodos propios de la teoría cinética y de la mecánica estadística.

El conocimiento de estas ecuaciones es fundamental para realizar el estudio termodinámico de un sistema ya que, a partir de ellas, pueden obtenerse todas las propiedades termodinámicas del mismo. Ahora bien, parte de la información que puede dispensar la ecuación energética de estado necesita la colaboración del primer principio de la termodinámica.

-Ecuación térmica de estado del gas ideal

Experimentalmente se encuentra que, a bajas presiones, la razón pv/T tiene el mismo valor, R, para todos los gases. Es conveniente postular entonces un gas ideal para el cual, por definición, la citada razón coincida con el valor límite que toma para los gases reales, a cualquier presión y tª. Así: pv=RT donde R es la llamada constante universal de los gases cuyo valor es R=8,3148E3 J/KmolxK

La ecuación recibe el nombre de ecuación térmica de estado del gas ideal o ecuación de Clapeyron.