Ecuaciones de estado (II)
-Gases reales
Cuando se compara el comportamiento de un gas real con el previsto por la ecuación de Clapeyron se observan en general, grandes discrepancias. Esto significa que la ecuación de Clapeyron no es la más adecuada para describir satisfactoriamente el comportamiento de los gases reales. Por esta razón, el estudio de los gases reales hace uso de cualquiera de los tres métodos alternativos siguientes:
• Se modifica la ecuación de Clapeyron de manera tal que refleje la realidad, es decir, el hecho de que un gas real es un sistema de partículas interaccionantes que poseen un volumen propio. Éste es el origen de las diversas ecuaciones térmicas de los gases reales.
• Se introduce en la ecuación de Clapeyron un facto, llamado de crompesibilidad que pone de manifiesto las discrepancias entre los resultados previstos por ella y los experimentales.
• Se define una nueva magnitud, la fugacidad, que desempeña en el estudio de los gases reales idéntico papel al de la presión en el estudio de los gases ideales.
De los 3 métodos alternativos, trataré sólo los 2 primeros.
-Ecuaciones térmicas de estado de los gases reales
Se han propuesto muchas ecuaciones que describen las relaciones p-v-T de los gases reales más exactamente que la ecuación de un estado de gas ideal. Alguna de estas ecuaciones son puramente empíricas, en tanto que otras se deducen de hipótesis sobre las propiedades moleculares. Entre las más utilizadas figuran las siguientes:
• Ecuación de van der Waals: 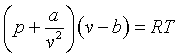
• Ecuación de Clausius: 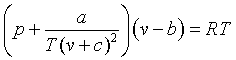
• Ecuación de Berthelot: 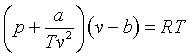
• Ecuación de Dieterici: 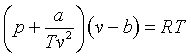
• Ecuación del virial: 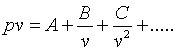
Evidentemente cualquiera de las ecuaciones anteriores puede proporcionarnos la siguiente información:
• Coeficientes térmicos de un gas real
• Coordenadas del punto crítico
-Ecuaciones térmicas de estado en forma reducida
La mayor parte de las ecuaciones térmicas de estado propuestas para explicar el comportamiento de un gas real son de la forma: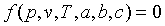
Donde a, b y c son parámetros característicos del gas. Ahora bien, si en la ecuación anterior expresamos los citados parámetros en función de las coordenadas críticas, entonces la ecuación anterior se transforma en: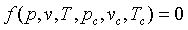
Y si finalmente, utilizamos las coordenadas críticas como unidades de presión, volumen y tª, definiendo coordenadas reducidas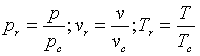
la ecuación adopta la forma 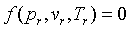
Es interesante observar que en esta ecuación ha desaparecido la impronta peculiar de cada gas reflejada, bien a través de los parámetros característicos o bien a través de las coordenadas críticas. En otras palabras, todos los gases que obedecen a la misma ecuación térmica de estado poseen una misma ecuación reducida. En este sentido se dice que la última ecuación tiene un carácter universal.
Se deduce igualmente que si las cantidades equimoleculares de dos gases cualesquiera se encuentran a igual presión reducida y ocupan el mismo volumen reducido, deberán encontrarse a la misma tª reducida (ley de los estados correspondientes).
