Sistemas de fuerzas
Hoy vamos a estudiar como pueden ser las fuerzas que actúan sobre un mismo cuerpo, es decir, vamos a estudiar los sistemas de fuerzas; ya que son el conjunto de fuerzas que actúan en un cuerpo a la vez.
A cada una de las fuerzas que forman el sistema de fuerzas se les llama componente del sistema. Llamamos resultante a una única fuerza cuyo resultado es el mismo que el que produce todo el conjunto de las fuerzas del sistema. Análogamente, llamamos equilibrante a la fuerza cuyo módulo es igual a la resultante pero es de sentido contrario.
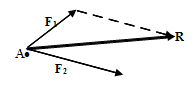
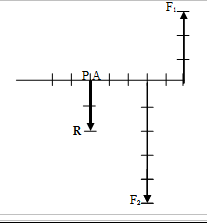
En la siguiente imagen podemos ver dos componente F1 y F2 que actúan sobre el cuerpo A, y cuya resultante es R.
Para calcular la resultante ( R ) representamos la segunda fuerza F2 haciendo coincidir el extremo de F1 con el origen de F2, de forma paralela a nuestra F2 inicial; tal y como podemos observar en la imagen anterior. La resultante, será el vector que une el origen de la primera fuerza, es decir, donde está situado nuestro cuerpo (A), con el extremo de F2.
Además, es importante mencionar que los sistemas de fuerzas pueden ser de dos tipos: concurrentes y no concurrentes. Los sistemas de fuerzas concurrentes son aquellos en los que todas las fuerzas se cruzan en un solo punto, mientras que en los sistemas de fuerzas no concurrentes, las fuerzas no se cruzan en un solo punto.
A continuación vamos a ver los diferentes sistemas de fuerzas que nos podemos encontrar según se presenten las fuerzas sobre los cuerpos.
FUERZAS QUE ACTÚAN EN EL MISMO SENTIDO
Cuando sobre nuestro cuerpo actúan dos fuerzas que tienen el mismo sentido, la intensidad de la fuerza resultante será la suma de las intensidades de las fuerzas, y tendrá el mismo sentido que ellas.
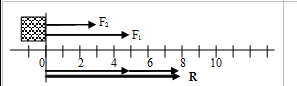
Ejemplo: Hallar la resultante de las siguientes componentes: F1=5N y F2=3N, las cuales actúan empujando el cuerpo hacia la derecha.
La resultante será: R=5N+3N=8N y el sentido de la fuerza será también hacia la derecha, como podemos ver en la siguiente imagen.
FUERZAS QUE ACTÚAN EN SENTIDOS CONTRARIOS
Si actúan sobre un cuerpo dos fuerzas de tienen sentidos contrarios, es decir, mientras una va hacia la derecha, el sentido de la otra es a la izquierda; entonces la intensidad de la resultante se obtienen restando las intensidades de las fuerzas. Mientras que el sentido de la resultante coincide con el sentido de la fuerza con mayor intensidad.
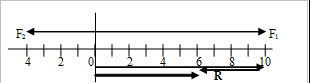
Ejemplo: Dadas las fuerzas F1=10N y F2=4N, de tal forma que la primera va hacia la derecha y la segundo hacia la izquierda, obtén la fuerza resultante:
Para calcular la resultante realizamos la siguiente resta: R=10N-4N= 6N. El sentido de la resultante coincidirá con el sentido de la primera fuerza, por tanto, hacia la derecha.
FUERZAS ANGULARES
Cuando actúan dos fuerzas sobre un mismo cuerpo de tal forma que sus direcciones forman un ángulo decimos que las fuerzas son angulares.
Para calcular la resultante, utilizamos lo que hemos comentado al principio del artículo. Es importante destacar que en este caso, la resultante no siempre será la suma de las intensidades de las fuerzas, sino que dependerá del ángulo que formen entre sí. Para calcular la resultante en este caso, se utiliza la ley del coseno.
FUERZAS PARALELAS EN EL MISMO SENTIDO
Cuando dos fuerzas actúan de forma paralela y en el mismo sentido, la intensidad de la resultante se calcula realizando la suma de las intensidades de las componentes. Y tendrá el mismo sentido que ambas fuerzas. Por último, el punto de aplicación será un punto entre medias de tal forma que F1xd1=F2xd2, encontrándose más cerca de la fuerza de mayor intensidad.
Ejemplo: Sean las fuerzas F1=12N y F2=9N que se encuentran separadas por 14 cm. Calcula la fuerza resultante y su punto de aplicación.
La intensidad de la resultante será: R = F1 + F2 = 12N + 9N = 21N
El punto de aplicación será la solución del sistema formado por estas dos ecuaciones: 12d1=9d2 y d1+d2=14. Entonces d1=6, es decir el punto de aplicación está a 6cm de F1.
FUERZAS PARALELAS DE SENTIDO CONTRARIO
Cuando dos fuerzas actúan de forma paralela y en sentido contrario, la intensidad de la resultante se calcula realizando la diferencia de las intensidades de las componentes. Tendrá la dirección de la componente de mayor intensidad y el punto de aplicación se calcula como en el caso anterior.
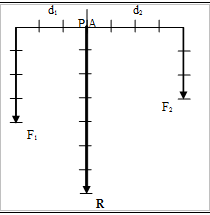
Ejemplo: Sean las fuerzas F1=12N y F2=20N, de tal forma que F1 va hacia arriba y F2 hacia abajo, calcula la intensidad de la resultante y su punto de aplicación. De tal forma que están separadas 10cm.
La intensidad será R = F2 – F1 = 20N – 12N = 8N.
La dirección será hacia abajo ya que la de mayor intensidad es F2.
El punto de aplicación al igual que en el caso anterior se obtendrá calculando el sistema formado por las siguientes ecuaciones: 12d1=20d2 y d1-d2=10.
Finalmente, es importante destacar que los sistemas de fuerzas son fundamentales en muchas áreas de la física y la ingeniería. Por ejemplo, en la mecánica de fluidos, los sistemas de fuerzas son utilizados para analizar las fuerzas que actúan sobre un fluido en movimiento. En la ingeniería estructural, los sistemas de fuerzas son utilizados para diseñar estructuras que pueden soportar cargas sin colapsar. Por lo tanto, entender cómo funcionan los sistemas de fuerzas es esencial para muchas disciplinas científicas y técnicas.