Introducción al Estudio de las Fuerzas
El peso es una fuerza
Cuando los cuerpos son abandonados en las proximidades del suelo, caen sufriendo variaciones de velocidad. Afirmamos entonces que la Tierra interactúa con esos cuerpos ejerciendo una fuerza la cual llamamos peso y que se indica con la letra P.
Algunos conceptos de la Fuerza Peso:
El peso de un cuerpo es la fuerza de atracción que la Tierra (o un planeta) ejerce en el cuerpo.
El peso de un cuerpo es la fuerza de atracción gravitatoria que la Tierra (o la Luna) ejerce en el cuerpo.
El peso es una Magnitud Vectorial
Cuando un cuerpo está en movimiento bajo la acción exclusiva de su peso P, el adquiere una aceleración denominada “aceleración de la gravedad g. Siendo m la masa del cuerpo, la ecuación fundamental FR = m . a se transforma en P = m . g, pues la resultante FR es el peso P y la aceleración es la aceleración de la gravedad.
Veamos:
|
FR = m . a |
|
P = m . g |
El peso P es una magnitud vectorial y tiene dirección siempre vertical (orientada hacia el centro de la Tierra) y con sentido desde arriba hacia abajo.
Es bueno recordar que:
El peso y la masa son magnitudes diferentes. La masa es una magnitud constante y no depende del lugar donde sea medida. El peso del cuerpo depende del lugar donde es medido.
Fuerza Elástica
Consideremos un elástico ligado en su extremidad superior. Aplicándose una fuerza F en la extremidad inferior del resorte el sufre deformación (x). Esa deformación se llama Elástica, cuando retiramos la fuerza F, el resorte retoma la misma posición.
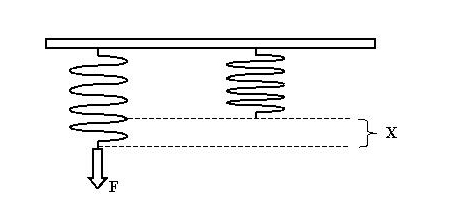
Llamaremos fuerza elástica, toda fuerza que tiene propiedades semejantes a la fuerza de la figura anterior.
El científico Inglés Robert Hooke ( 1635-1703) estudió las deformaciones elásticas y llegó a la siguiente conclusión:
En un régimen de deformación elástica, la intensidad de la fuerza es proporcional a la deformación.
F = k . X
| K | Contante elástica del resorte |
| X | Deformación del resorte |
Fuerza de Rozamiento
Consideremos un cuerpo sobre una superficie horizontal, en la cual actúa una fuerza F horizontal, insuficiente para trasladarlo.
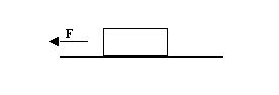
Como el cuerpo continúa en reposo, la resultante de las fuerzas que actúan sobre el debe ser nula.
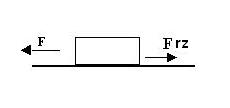
Como puede ser observado, esto no podría suceder pues aparentemente, en la dirección horizontal solo existe fuerza F (elástica) actuando en el cuerpo. Entonces somos obligados a admitir la existencia de una fuerza opuesta a la tendencia del movimiento. Tal fuerza es llamada como Fuerza de Rozamiento Frz.
Tipos de Fuerza de Rozamiento
Existen dos tipos de fuerza de rozamiento:
- Estática
- Dinámica
Fuerza de Rozamiento Estática
Es aquella que actúa en tanto no ocurre movimiento. Mientras el rozamiento es estático, a medida que aumentamos la fuerza motriz F, la fuerza de rozamiento Frz también aumenta, de forma de equilibrar la fuerza e impedir el movimiento. Pero la fuerza de rozamiento no crece indefinidamente, sino que llega a un valor máximo que se llama Fuerza de Rozamiento de Destaque Frzd.
Fuerza de Rozamiento Dinámica
Es aquella que actúa durante el movimiento. Para iniciar el movimiento, partiendo del estado de reposo, es necesario que la intensidad de la fuerza motriz F sea superior a la intensidad de la Fuerza de Rozamiento de Destaque Frzd.
Una vez iniciado el movimiento, la fuerza de rozamiento estática deja de existir, pasando a actuar la fuerza de rozamiento dinámica, también contraria al movimiento y de valor inferior al de la fuerza de rozamiento de destaque.
Expresiones Matemáticas
Frz = µE . N
( cuerpo en reposo )
µE … Coeficiente de rozamiento estático.
Frz = µ D . N
( cuerpo en movimiento )
µD … Coeficiente de rozamiento dinámico
OBS.: Cuando el plano de apoyo es horizontal, el peso P es igual a la fuerza normal N.
|
P = N |
|
Frz = µ . N |
|
Frz = µ . P |
|
Frz = µ . m . g |
Atención:
La fuerza de rozamiento independe del área de contacto entre las dos superficies. La Fuerza de rozamiento independe de la naturaleza de la superficie de contacto (pulida, lubricada, etc).
El coeficiente µ es a-dimensional (no tiene unidad de medida) y depende apenas de las superficies de contacto.
