Impulso mecánico, equilibrio dinámico y fuerzas de inercia.

—> Impulso mecánico

Otro modo de explicar la expresión del Principio fundamental de la dinámica de traslación es que el impulso mecánico es igual a la variación del momento lineal. Es decir: I= p_final-p_inicial = m·v-m·v_o = m·(v–v_o) = –> I=Δp.

La variación de momento lineal, que experimenta una partícula (Δp) no sólo depende de la fuerza que actúa sobre ella, sino también del tiempo (Δt) durante el cual actúa.

La ecuación que propone la citada Segunda Ley de Newton es: Δp/Δt = F y despejando Δp se tiene: Δp = F·Δt. El producto F·Δt (fuerza aplicada multiplicada por el tiempo que dura su actuación) se denomina impulso mecánico.

Se trata de una magnitud vectorial, de la misma dirección y sentido que los de la fuerza aplicada, y cuyo valor es el producto de la fuerza por el tiempo. Su ecuación de dimensiones es: [I]=M·L·T^-2·T=M·L·T^-1 y su unidad en el sistema internacional es Kg·m/s (newton por segundo). De forma más correcta, como las fuerzas son variables en el tiempo, debemos sumar todos los diferenciales de tiempo mediante una integral. Así que escribimos: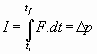

—> Equilibrio dinámico y Fuerzas de inercia

Cuando vamos en un coche y se frena bruscamente o cuando se toma una curva, notamos que sobre nosotros actúa una fuerza dirigida en sentido contrario al movimiento que nos impulsa la cabeza. Este fenómeno se observa siempre que un sistema esté sometido a una aceleración y en él existen partes móviles (que pueden moverse con mayor o menor grado de libertad). A esas fuerzas aparentes se las llama fuerzas de inercia. Así que podemos enunciar:

Siempre que una fuerza produzca una aceleración a un sistema, se originará en las partes móviles del mismo otra fuerza igual y opuesta a la primera.

En este caso se dice que el sistema se encuentra en equilibrio dinámico ya que las fuerzas «ficticias» de inercia contrarrestan el efecto de las debidas a la aceleración «real». Por lo tanto tenemos que F + F_i = 0 y:

Principio de d»Alembert

En todo sistema en equilibrio dinámico la suma de las fuerzas que actúan, incluidas las de inercia, es cero.

NOTA: las variables en negrita son vectoriales. La variables sin negrita son escalares.