Mecánica vectorial
Considere en un plano la existencia de un avión y dos líneas perpendiculares, una de ellas horizontal y la otra vertical. Al eje horizontal se le llama la abscisa (o eje OX) y al vertical se le llama eje y (o eje OY).
Los pares ordenados de puntos en el plano se indican en la forma general P = (x, y) donde x es la abscisa del punto P al punto P.
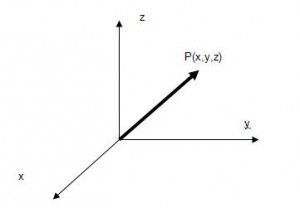
De hecho, x representa la distancia entre las dos líneas verticales que aparecen en la gráfica y la distancia entre las dos líneas horizontales que se muestran en la tabla.
El sistema de coordenadas ortogonales es también conocido como sistema de coordenadas cartesianas.
Este sistema tiene cuatro regiones llamadas cuadrantes.
Valor de Pitágoras
En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos y c.
A 2 = b 2 + c 2
Distancia entre dos puntos en el plano cartesiano
Con los puntos P = (x 1, y 1) y Q = (x 2, y 2), obtenemos la distancia entre P y Q, mediante el trazado de las proyecciones de estos puntos en los ejes de coordenadas y la identificación de un triángulo en el gráfico, desde allí, usamos el Teorema de Pitágoras.
El segmento PQ es la hipotenusa del triángulo PQR, el segmento PR es una pierna y QR segmento es la otra pierna, por lo tanto:
[D (P, Q)] 2 = [d (P, R)] 2 + [d (Q, R)] 2
Y cómo:
[D (P, R)] = 2 | x 1 – x 2 | 2 = (x 1 – x 2) 2
[D (Q, R)] = 2 | y 1 – y 2 | 2 = (y 1 – y 2) 2
A continuación, algunos ejemplos
La distancia entre P = (2,3) y Q = (5.12) es
d (P, Q) =
La distancia entre el origen O = (0,0) y un punto genérico P = (x, y) está dada por
d (O, P) =
Punto medio de un segmento
Los puntos P = (x 1, y 1) y Q = (x 2, y 2), se pueden obtener en el punto medio M = (x m, y) que se encuentra entre P y Q, usando una media aritmética, una de las abscisas y las ordenadas del otro.
m x = (x 1 + x 2) / 2
y = f (y 1 + y 2) / 2
Tenga en cuenta:
El centro de gravedad de un triángulo cuyo vértice plano de coordenadas son A = (x 1, y 1), B = (x 2, y 2) y C = (x 3, y 3) está dada por:
G = ((x 1 + x 2 + x 3) / 3 (y 1 + y 2 + y 3) / 3)
Desde el punto de vista de la geometría euclidiana, dados dos puntos P 1 = (x 1, y 1) y P 2 = (x 2, y 2) en el plano cartesiano, no hay una sola línea a través de estos puntos. Para determinar la ecuación de una línea hay una necesidad de información y esta radica en dos conceptos importantes: la pendiente de la línea y el coeficiente lineal.
Pendiente de una línea
Teniendo en cuenta los puntos P 1 = (x 1, y 1) y P 2 = (x 2, y 2), 1 x x2, la pendiente de la línea a través de estos puntos es el número real.
