Aceleración angular
Definimos aceleración angular como los cambios que experimenta la velocidad en las unidades de tiempo. Hacemos referencia a ella con la letra griega alfa α. Igual que la velocidad angular, la aceleración es de una corriente vectorial.
Se define aceleración angular como el canje que sufre la velocidad en las unidades de tiempo. Se la denomina como alfa α. Así como la velocidad angular, la aceleración angular presenta carácter vectorial.
La expresamos en s-2 que representa los radianes por segundo al cuadrado y esto es porque el radián es adimensional. Por ende la aceleración angular mantiene el eje de rotación que se mantiene en una dirección constante en el espacio.
Definimos como vector de aceleración angular en su ecuación como
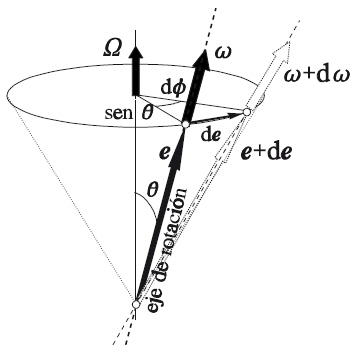
El vector de velocidad angular de un cuerpo contorno del eje de rotación lo denominamos e y al versor asociado de dicho eje se denomina w, del modo que tenemos w = we.
En el caso individual en que este eje de rotación mantiene su orientación fija, el espacio entonces será de/dt = 0 y su vector asociado en este caso alfa, se localiza referente el eje de rotación. Implementándose de la siguiente manera:
De esta forma el módulo de la aceleración angular |α| = α, como la derivada de la aceleración angular respecto al modo angular del tiempo, su dirección es aquella que corresponde al eje de rotación. Por otro lado el sentido es la w cuando la aceleración angular se incrementa con el tiempo, pero a su vez el sentido opuesto comienza a disminuir.
Cuando el eje de rotación no conserva la dirección precisa en el espacio será sin embargo
porque el versor de este eje cambia de dirección por el transcurso en el que el movimiento de e es un versor, la derivada se presentará como un vector perpendicular a e, todo ello respecto al eje instantáneo de rotación.
En ese caso lo más general de aceleración angular de alfa que se expresa de la siguiente manera
Siendo gama la velocidad angular referida a la rotación o precesión de este eje de rotación. En la fórmula debemos observar que el vector aceleración tiene dos componentes básicos. Los dos componentes longitudinales cuyo módulo es .
Los componentes transversales, perpendiculares al eje rotación cuyo módulo gama x W son la segunda característica de este tipo de cálculos.
El vector de expresión anterior que observamos denominado alfa no presentará similar dirección y aceleración que el vector W.
El vector de aceleración angular alfa no tendrá por ende una dirección en su eje de rotación.
En los movimientos planos de un sólido rígido la aceleración angular al igual que la velocidad, tienen una dirección de eje de rotación y es dado por:
La función de la velocidad angular se puede observar a:
Esperamos que mediante el uso de este artículo te hayan quedado claro que las funciones planteadas para ser utilizadas deben ser implementadas en el sentido de que no hay una muy buena relación entre los teoremas y los axiomas por lo que recomendamos basarse en las situaciones en que lo elementos pre indicados puedan ser llevados al cociente de la moción.
