Una de momentos (II) – Momento cinético o angular. Momento de inercia.

Hablemos de los distintos momentos de rotación que encontramos en la dinámica de una partícula o de un sistema.

Escribiremos el producto escalar con un punto (·), y el producto vectorial con una cruz (x). Las magnitudes en negrita son vectoriales y las que no están en negrita son escalares.

Momento angular o cinético (L):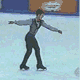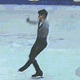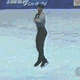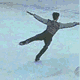

Se define el momento angular o cinético de una partícula como el producto vectorial del radiovector que fija la posición de la partícula en cada instante por el momento lineal que posee dicha partícula. Es decir, L = r x P. Como P viene definida por P=m x v, el momento angular podría decirse que es el momento del propio momento lineal y se escribe como: L=m·r x v.

Esto es lo mismo que: L=r·m·v·senα, siendo α el ángulo r (radio de la figura, del origen al extremo que dibuja la trayectoria) y v (velocidad, tangente a la trayectoria). Éstos son perpendiculares normalmente y sen90º=1, por lo tanto L toma la dirección perpendicular al plano definido por ambos (r y v).

En un sistema de partículas, L del centro de masas equivale a la suma vectorial de los momentos angulares de todas las partículas del sistema.

Teorema del momento angular:

La derivada respecto al tiempo del momento angular de un sistema que se mueve en relación a un punto material es igual al momento, respecto a dicho punto, de las fuerzas exteriores que actúan sobre el sistema. Es decir: M_ext=δL/δt. Llegamos a esta conclusión pues:

δL/δt = [(δr/δt) x (mv)] + [r x (δmv/δt)] = [v x (mv) + (r x F)] = 0 + r x F = M.

Principio de conservación del momento angular:

«Si el momento, respecto a un punto, de las fuerzas exteriores (o la dirección de r y F coinciden) que actúan sobre un sistema es nulo (aislado), el momento angular respecto al mismo punto permanece constante».

Es decir, que el momento angular de un sistema aislado es constante. Es sencillo verlo pues si no actúan fuerzas sobre él M será nulo, y para que M=δL/δt sea nulo, L debe ser constante.

Un ejemplo práctico para verlo es el caso del patinador.

Un patinador, como el de la foto de arriba, extiende los brazos al final de un giro. ¿Qué efecto produce? Pues sencillo. Sabiendo que el momento angular del sistema es constante, al aumentar el radio (r) de la figura (extendiendo los brazos), la velocidad debe disminuir con tal de que el producto final permanezca igual que como estaba. Así el patinador consigue acelerar su giro cerrando los brazos y frenar su velocidad al terminar el giro.

Momento de Inercia (I):

Supongamos un sólido rígido capaz de girar alrededor de un eje vertical z. Consideremos, asimismo, que en un punto cualquiera del sólido se aplica una fuerza F de dirección arbitraria que, lógicamente, puede descomponerse en dos. Una en la dirección del radio que une el eje con el punto y que es anulado por la resistencia del eje, y otra perpendicular a la primera que producirá un movimiento de rotación. Como hemos definido antes, L=m·r x v, y como sabemos de cinemática de rotación: v=ω·r. Por lo tanto, L=m·r²·ω. Pues al producto de masa por la distancia del eje al cuadrado (r²) se le llama momento de inercia I. Así pues se puede expresar el momento angular como: L=I·ω.

El terorema de conservación del momento de inercia en rotación propone que L=I·ω es constante en todo sistema aislado (como vimos en el momento angular).

Ecuación Fundamental de la Dinámica de Rotación:

M=I·α

Análoga a la Ecuación Fundamental de la Dinámica de Traslación (F=m·a tenemos ésta, donde M es el momento de una fuerza, I el momento de inercia y α la aceleración angular. Viene de derivar L=I·ω. (δL/δt)=[(δI/δt) · ω] + [I · (δω/δt)]. El primer término es cero ya que I es constante porque el sólido gira alrededor de un eje concreto, así que: (δL/δt)=I·α = M.