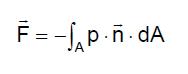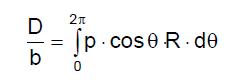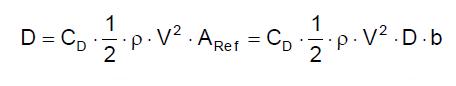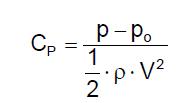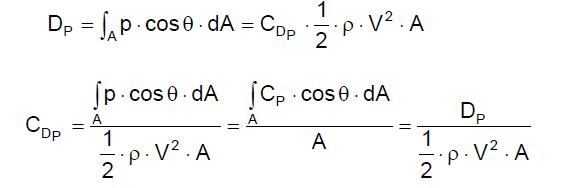Coeficiente de Presión
Para un cuerpo inmerso en un fluido, donde hay movimiento relativo entre ambos, surge una fuerza resultante de esta interacción. Es usual expresar esta fuerza en función de dos componentes llamados Fuerza de Arrastre (D o FD) y de Fuerza de Sustentación (L o FL), que poseen respectivamente dirección paralela a la de la velocidad del fluido en la distancia (Fuerza de Arrastre) y dirección perpendicular a la de la velocidad en la distancia (Fuerza de Sustentación).
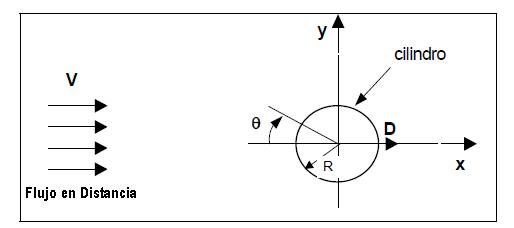
Inclusive siendo el cilindro estudiado tridimensional, se adopta en este análisis una simplificación, haciéndolo bidimensional, conforme vemos en la figura a continuación:
Representación del flujo en torno a un cilindro y sus referencias.
Una consecuencia de este análisis bidimensional es considerar estas fuerzas por unidad de longitud, que en el caso del cilindro será por unidad de altura (b).
En términos generales, la interacción fluido-cuerpo, es descrita por fuerzas de superficie (contacto) asociada a las tenciones tangenciales (corte) y las tensiones normales, que se identifican con la distribución de presiones sobre la misma.
La integración de la distribución de las tensiones de corte y de las presiones sumadas resultarán en la Fuerza Resultante (F) con componentes de arrastre (D) y de sustentación (L).
En nuestro caso serán despreciadas las contribuciones de la tensiones tangenciales (rozamiento viscoso) y será realizada la integración de las presiones, entonces:
La simetría del cilindro y de los respectivos componentes de la fuerza resultante de la distribución de las presiones en la dirección y, dirección en que está orientada la sustentación, indica que en este caso es probable de obtenerse un componente de la fuerza de sustentación igual a cero (L = 0).
Entonces, el foco del estudio se dirige hacia la fuerza de arrastre (D) que está en la dirección x y está dado por:
Tomando por unidad de altura (b) del cilindro se tiene que:
donde R es el radio del cilindro y θ es el ángulo tomado en relación a la dirección x.
La integración de la ecuación anterior puede ser realizada de forma discreta tomándose la sumatoria de las contribuciones de la presión sobre áreas definidas por intervalos angulares Δθ variándose θ apenas de 0 a π y multiplicándolo por 2. Esto porque está considerada la simetría del fenómeno en relación al eje x.
Pero la fuerza de arrastre también puede ser determinada por la relación que utiliza el coeficiente de arrastre (CD):
en la cual
- ½. ρ . V2 expresa la presión dinámica de escape en distancia
- V es la velocidad en distancia
- ARef es el área adoptada como referencia, en este caso se adopta AREF = d . b (área proyectada del cilindro en plano transversal al escape).
- CD es el coeficiente de arrastre (adimensional)
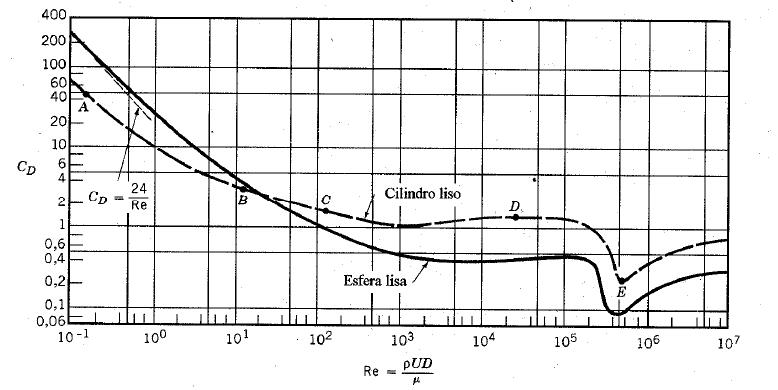
El coeficiente de arrastre CD, puede ser determinado experimentalmente y es usual presentar sus valores de forma gráfica en función de otro parámetro adimensional, el número de Reynolds (Re), que representa las condiciones de escape, conforme puede ser visto a continuación:
Coeficiente de arrastre en función del número de Reynolds
El coeficiente de Presión
La distribución de presiones sobre la superficie del cilindro puede ser explicada a través de un parámetro identificado como Coeficiente de Presión (CP) y surge de la expresión:
En la cual:
p = p (θ) es la presión en cada punto de la superficie del cilindro
po es una presión de referencia, en general adoptada como presión estática en el flujo en distancia.
Este coeficiente de presión también puede ser asociado a la fuerza de arrastre (Dp) y al coeficiente de arrastre (CDp) relativos a la presión:
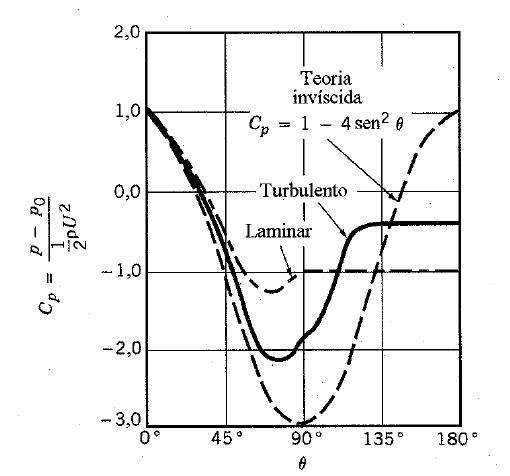
Los valores para el coeficiente de presión (CP) en función de θ son obtenidos a partir de resultados experimentales para diferentes condiciones de escape, usualmente caracterizados por el número de Reynolds (Re), conforme vemos en la figura a continuación. En ella está representado, también el comportamiento de CP determinado teóricamente considerando el escape de fluido no viscoso.
Coeficiente de presión en función del ángulo