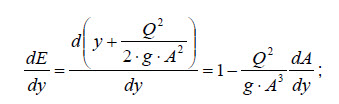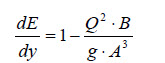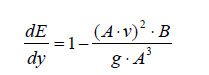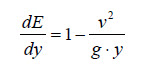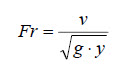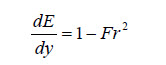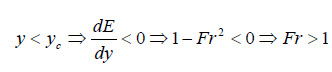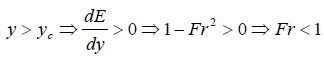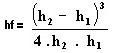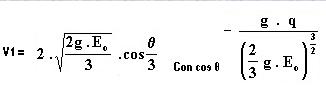Número de Froude
Para obtener el punto crítico (punto de mínima energía del flujo libre), se deriva la ecuación de energía específica en función de la profundidad de la siguiente forma y se iguala el resultado a cero, con el desarrollo de la siguiente forma:
Siendo que dA = B.dy, se obtiene que:
Reescribiendo la última ecuación a partir de la aplicación de la ecuación de continuidad:
Donde:
Q es el caudal del canal de drenaje
V es la velocidad media del flujo
A es la zona húmeda es la sección transversal
Tenemos que:
Haciendo B = A/y, obtenemos que:
A partir de esta expresión, se define una magnitud adimensional denominada Número de Froude (Fr) igual a:
Combinando las dos últimas expresiones obtenemos que:
En el flujo crítico, cuando la energía específica es mínima dE/dy = 0, el Fr = 1.
Evaluándose la variación de dE/dy en las diferentes profundidades de escorrentía podemos escribir:
Caracterizando el flujo supercrítico
Caracterizando el flujo subcrítico
El número de Froude es un adimensional importante en la Física Hidráulica, permitiendo el establecimiento de diferentes interpretaciones.
La condición crítica de escorrentía corresponde al límite entre los regímenes fluvial y torrencial. De esta forma siempre que ocurren cambios en el régimen de escorrentía, la profundidad debe pasar por su valor crítico.
Este pasaje sin embargo, puede ocurrir de forma gradual o brusca, de acuerdo con el régimen de escorrentía de montante y con la singularidad que provoca la variación.
Diversas situaciones prácticas nos permiten observar el cambio del régimen de flujo. Son ejemplos del pasaje del régimen subcrítico hacia el supercrítico:
- Paso de una pendiente subcrítica para una pendiente supercrítica
- Caída libre a partir de una pendiente ascendente crítica
- Escorrentías a lo largo de la cresta de vertederos
- Estrechamiento o alargamiento de la sección
- Escalón en el fondo del canal
El cambio de régimen supercrítico hacia el subcrítico es observada, por ejemplo en cambios en la pendiente y en salidas de las compuertas. El flujo en régimen crítico (o en sus inmediaciones) es inestable.
Así el menor cambio de energía específica provocaría un sensible cambio en la profundidad del agua del canal.
Se puede verificar fácilmente que en el régimen crítico la carga cinética es igual a la mitad de la profundidad media.
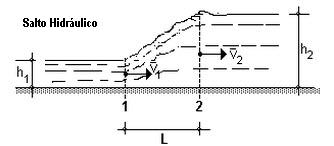
Energía Hidráulica disipada y gradientes de velocidad
El salto hidráulico es un fenómeno que se produce cuando la corriente líquida pasa del régimen supercrítico o rápido para el subcrítico o tranquilo, pasando a lo largo de su desarrollo por el punto crítico de escorrentía. Para que exista salto la condición necesaria debe ser:
Donde:
Es el número de froude en la sección “i” del salto (de William Froude, 1810-1879, matemático e ingeniero civil inglés).
La energía hidráulica disipada debida al gradiente de velocidad que promueve la mezcla rápida puede ser calculada por la fórmula de Bélanger (Jean-Baptiste Bélanger, 1789-1874, notable físico hidráulico francés).
Para números de Froude comprendidos entre 4,5 y 16,0 por ejemplo, la extensión del salto podrá ser estimada por la expresión:
L = 6,5 (h2 – h1)
Con la potencia P = g . Q . hf , entonces
Donde el tiempo de mezcla T es:
T = 2L / (V2 + V1)
Vi= velocidad media en la sección “i” en m/s,
g= peso específico del líquido, en m3/s,
m= coeficiente de viscosidad.
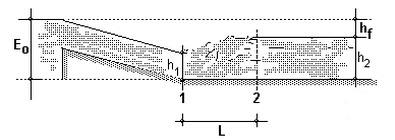
Un cambio brusco en la pendiente en un canal regular es uno de los medios más simples de producir un salto hidráulico con la finalidad de efectuar una mezcla rápida. En este caso de resaltos provocados por cambios en el declive del canal tenemos:
E0 = E1 = V12 /2g + h1 con h1 = Q / (B.V1) = q / V1
Donde B es el ancho del canal y q = Q/B y por tanto el flujo o unidad específica. Subtituyendo h1 tenemos en función de E0: