Número de Rayleigh

Vamos a analizar la convección con más cuidado. En estado de equilibrio, la temperatura es la misma en las dos superficies del líquido y es igual a la temperatura externa. En equilibrio el líquido es uniforme e en el lenguaje de los físicos, es invariante para todas las transacciones y rotaciones.

Este equilibrio también es estable. Después de una perturbación local de la temperatura, el sistema vuelve al estado uniforme, de acuerdo con la Segunda Ley de la Termodinámica.

Si aumentamos ligeramente la temperatura de la superficie inferior, un flujo continuo de energía pasa a través del líquido. El sistema conduce el calor de la superficie caliente hacia la superficie fría, a través de la redistribución de la energía a nivel molecular.

El líquido es no-uniforme: la temperatura, la densidad y la presión en el interior del líquido varían linealmente entre las dos superficies. La estructura de conducción es impuesta por las condiciones externas y no es una estructura autoorganizada.

Si aumentamos progresivamente la temperatura, existe un umbral a partir del cual el comportamiento del líquido cambia drásticamente: Aparecen células de convección cuya sección está presentada en la figura a continuación

El movimiento microscópico aleatorio de las moléculas se ordena espontáneamente al nivel macroscópico, con una longitud de correlación característica.

Este orden ocurre en una escala de milímetros, muchos ordenes de magnitud superior a la escala microscópica que caracteriza el orden de casi todos los sistemas en equilibrio.

Células de convección, vista desde arriba

 

Mecanismos Estándar de Convección

Este patrón dinámico formado por rollos de convección en que la rotación del fluido en las células alterna entre el sentido de las agujas del reloj y el sentido opuesto a medida que nos movemos en la horizontal, es estable: una pequeña perturbación no altera el estado del sistema

Además de ello, aunque pequeñas variaciones de las condiciones experimentales puedan hacer variar el arreglo particular del patrón, haciendo con que una posición particular del líquido pueda estar en una célula que rueda en el sentido de las agujas del reloj o en una célula que rueda en el sentido opuesto en experiencias diferentes, las características globales del estándar son siempre las mismas, en la misma región de valores de la diferencia de temperatura.

Al atravesar el umbral de convección se da una rotura espontánea de simetría: Un patrón particular, con un tamaño característico, es seleccionado de forma que la simetría del estado de convección es la simetría del estado uniforme (líquido homogéneo) son diferentes y la de aquel es menor.

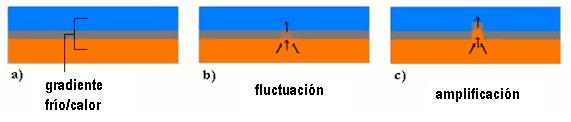
a) gradiente de temperatura b) una fluctuación calienta el líquido en una zona localizada y la diferencia de presión lo hace subir c) este movimiento del líquido deja espacio libre que es ocupado por líquido del fondo, más caliente, ampliando la fluctuación.

 

Lord Rayleigh estudió el origen de este patrón y mostró que las características que lo determinan (gradiente de temperatura, viscosidad y conductividad térmica del líquido) pueden ser combinadas en un único parámetro, el número de Rayleigh.

El número de Rayleigh es una medida del balance entre las fuerzas que promueven la convección (diferencia de densidad entre el líquido caliente y frío) y las que se le oponen (fricción debido a la viscosidad y la difusión térmica que opera en el sentido de anular el gradiente de temperatura).

El umbral de convección está dado por el valor del número de Rayleigh Ra=1708 relación entre la anchura y la altura de las celdas (vector de onda) en este punto es del orden de uno, de forma que los rollos tienen una sección aproximadamente cuadrada. Por encima de este umbral no existe apenas uno sino varios vectores de onda posibles y la determinación de la forma de las células requiere de un análisis más sofisticado.

Por ejemplo para ciertos valores de los parámetros por encima del umbral de convección, las células de convección se acomodan en un espectacular padrón hexagonal como lo ilustrado en la figura a continuación:

Células de convección hexagonales

 

En ella, el movimiento ascendente del líquido se da a lo largo del centro de los hexágonos y el descendiente a lo largo de las caras. Fue este el padrón que Bénard observo en 1900, en las experiencias que motivaron los trabajos teóricos de Rayleigh.

Hoy en día se sabe que muchas experiencias, incluyendo las del propio Bénard, en que la superficie enfriada del líquido está libre, el mecanismo que compite con la viscosidad y la difusión térmica para promover la convección no es debido a las variaciones de densidad con la temperatura, como en el modelo de Rayleigh, pero si a las variaciones de tensión superficial con la temperatura.

Ambos mecanismos de convección dan origen a las inestabilidades responsables por la quiebra de simetría y por la aparición de padrones.