Estructura cristalina y redes de Bravais (II)
Ayer veíamos una serie de definiciones que nos ayudaban a entender cómo se estudian los sistemas cristalinos. Vamos a ver ahora qué tipos de redes cristalinas hay tanto en 2 como en 3 dimensiones.
Redes en 2 dimensiones
Redes cristalinas en dos dimensiones podemos formar todas las que queramos, pues la longitud de los vectores de traslación de la base o el ángulo que forman es completamente arbitrario. Sin embargo no todas serán redes de Bravais. Existen únicamente 5 posibles redes de Bravais en dos dimensiones, que tenemos en la imagen de la derecha.
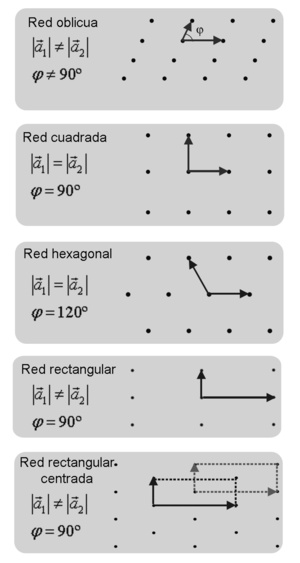En la red oblicua tenemos una base en la que el módulo de los dos vectores es distinto. Además, el ángulo φ que forman no es de 90º.
Para le red cuadrada, el requisito que se debe de cumplir es que el módulo de ambos vectores sea el mismo y que el ángulo que formen sea recto, es decir 90º. Éste es el tipo de red más sencillo.
La red hexagonal tiene, como su propio nombre indica, una estructura de hexágonos y por tanto no tenemos un ángulo recto sino que el ángulo entre los vectores de la base es de 120º. Además, los módulos de ambos vectores deber ser iguales.
La red rectangular es una pequeña modificación de la red cúbica. En este caso, en lugar de tener los módulos de los dos vectores iguales, son diferentes. En cuanto al ángulo, obviamente sigue siendo de 90º.
Por último tenemos la red rectangular centrada. Es exactamente igual que la red rectangular, con los módulos de los vectores diferentes y un ángulo de 90º, pero con el añadido de contar con un punto extra en el centro del rectángulo. Se puede ver también como una red hexagonal con los módulos de los vectores distintos. De hecho, es así como se forma su celda primitiva.
Estos son todas las posibles redes de Bravais para una estructura bidimensional.
Redes en 3 dimensiones
Una vez vistas las redes en 2 dimensiones pasemos a las 3 dimensiones. Aquí en lugar de tener dos vectores pasamos a tener ya tres y la cosa se complica algo más. Y ya no tenemos únicamente 5 redes de Bravais, sino que el número se incrementa hasta las 14, repartidas en 7 tipos diferentes de estructuras cristalinas.
Debido a la dificultad en el estudio de todas de estas redes vamos a indicar primero los 7 tipos diferentes que tenemos, y luego veremos algunas de las redes de Bravais más simples que son aquellas procedentes del sistema cúbico.
| Sistema Cristalino | Número de redes | Ejes | Angulos entre ejes |
| Cúbico | 3 | a1 = a2 = a3 | α = β = γ = 90° |
| Tetragonal | 2 | a1 = a2 ≠ a3 | α = β = γ = 90° |
| Ortorrómbico | 4 | a1 ≠ a2 ≠ a3 | α = β = γ = 90° |
| Hexagonal | 1 | a1 = a2 ≠ a3 | α = β = 90° ; γ = 120° |
| Trigonal (o Romboédrica) | 1 | a1 = a2 = a3 | α = β = γ ≠ 90° ; < 120º |
| Monoclínico | 2 | a1 ≠ a2 ≠ a3 | α = γ = 90° ≠ β |
| Triclínico | 1 | a1 ≠ a2 ≠ a3 | α ≠ β ≠ γ |
El sistema cúbico, como se puede ver en la tabla posee tres redes diferentes. Son las más sencillas de observar y son las que trataremos a continuación.
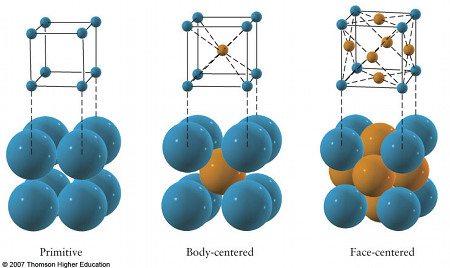
La mas simple es la red conocida como SC o Simple Cubic. No es más que un cubo con átomos en sus vértices. A partir de éste se forman los otros dos de una forma muy sencilla. Si a este cubo le añadimos un átomo en su centro pasamos a tener una estructura conocida como BCC o Body Centered Cubic. Un ejemplo de este tipo de sistema cristalino es el que forma el cloruro de cesio (CsCl). Si en vez de colocar un átomo en el centro del cubo lo colocamos sobre las caras tenemos una estructura FCC o Face Centered Cubic. Un ejemplo es el cloruro sódico (NaCl) o sal común.
Existen más tipos de redes muy importante y comunes como pueden ser el diamante o la hexagonal compacta HCP o Hexagonal Close Packet, pero ya son más complicadas de tratar.