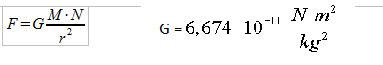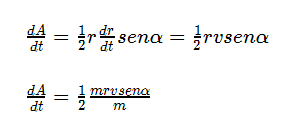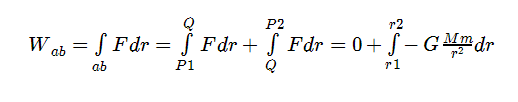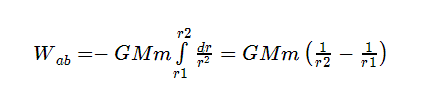Fuerza gravitatoria
Son muchos los post que hay sobre la ley de la gravitación universal, pero en esta ocasión nos vamos a centra en estudiar las propiedades de la fuerza gravitatoria.
Recordaremos en primer lugar cual era la fórmula de la fuerza gravitatoria que nos proporciona la ley de Newton de la gravitación universal.
Definicion: La fuerza gravitatoria que una masa puntual M ejerce sobre otra masa puntual m que se encuentra a una distancia r de la anterior es directamente proporcional al producto de las masas e inversamente proporcional al cuadrado de las distancias que las separa. Por tanto, viene dada por la siguiente expresión, donde G es una constante universal:
PROPIEDADES DE LA FUERZA GEAVITATORIA
A partir del estudio de la fórmula anterior podemos deducir las siguientes propiedades:
a) Es una fuerza de largo alcance. Teóricamente solo se anulará si las masas están separadas por una distancia infinita, aunque a efectos prácticos, no es necesaria una distancia tan grande para que, en algunas situaciones, sus valores se consideren despreciables.
b) Es independiente del medio en que se encuentran las masas. Como la constante G de gravitación universal tiene un valor constante, hace que la interacción gravitatoria sea la menos intensa de todas las interacciones fundamentales.
Además, es importante mencionar que la fuerza gravitatoria es siempre atractiva, es decir, las masas siempre se atraen entre sí. Esto es diferente de otras fuerzas fundamentales, como la electromagnética, que puede ser tanto atractiva como repulsiva. Esta propiedad de la fuerza gravitatoria es lo que mantiene a los planetas en sus órbitas y a los objetos en la superficie de la Tierra.
c) Es una fuerza central ya que actúa según la línea que une las masas que interaccionan. La segunda ley de Kepler es una consecuencia de este hecho. En efecto, supongamos un planeta P que en un cierto instante se encuentra en la posicion r respecto al Sol. Transcurrido un tiempo dt habrá sufrido un desplazamiento dr y el vector que le une al Sol habrá barrido la siguiente área por unidad de tiempo, es decir, la velocidad areolar del planeta es:
Donde la segunda fórmula se obtiene al multiplicar y dividir por la masa del planeta.
No obstante, el momento angular del planeta respecto al Sol es Ls= mr x v, por tanto su módulo será Ls= mrvsenα, donde α representa el ángulo de desplazamiento. A partir, de lo anterior, la ecuación del área vendrá dada de la siguiente manera: dA/dt=Ls/2m.
Y dado que la fuerza sobre el planeta es central, su momento respecto al Sol y el momento angular del planeta es constante, de forma que: dA/dt=constante. Esto último no es otra cosa que la ley de Kepler de las áreas, que nos dice que un planeta en su movimiento alrededor del Sol barrerá áreas iguales en tiempos iguales. Dicho de otro modo, que un planeta se mueve en torno al Sol con velocidad areolar constante.
d) Es una fuerza conservativa: el trabajo realizado por la fuerza gravitatoria para trasladar una partícula entre dos puntos es independiente del camino seguido. Efectivamente, si elegimos dos trayectos distintos, ab y cd, para llevar la masa m desde el punto P1 al punto P2 bajo el efecto gravitatorio de la masa M. El trabajo que la fuerza gravitatoria realiza sobre m por el camino ab se calcula como:
Ya que a lo largo del arco P1Q la fuerza y el desplazamiento son perpendiculares y en el tramo radial Qp2 tienen sentidos opuestos. Por tanto:
Análogamente ocurriría con el trabajo por el camino cd, obteniendo la misma expresión. Luego, como cualquier camino entre P1 y P2 puede descomponerse en una sucesión de pequeños trazos radiales y angulares, el trabajo para trasladar a m entre ambos puntos será independiente del camino seguido.
Además, la fuerza gravitatoria es una fuerza de campo. Esto significa que cada objeto con masa genera un campo gravitatorio a su alrededor, y cualquier otro objeto con masa que entre en este campo experimentará la fuerza de gravedad. Este concepto de campo es fundamental para entender la teoría de la relatividad general de Einstein, que describe la gravedad no como una fuerza, sino como la curvatura del espacio-tiempo causada por la masa y la energía.