Magnitudes acústicas (I)
En este post intentaré definir una serie de magnitudes características del campo acústico. Antes que nada, vamos a establecer la definición de valor eficaz de una magnitud. Se define, el valor eficaz de una magnitud Mef, en el intervalo de tiempo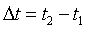 
, de la siguiente manera:
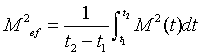
Se puede comprobar que, para una función sinusoidal del tiempo, el valor eficaz está relacionado con el valor máximo de la magnitud:
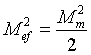. En el caso de que tengamos ondas esféricas, la expresión de la presión va a ser ligeramente diferente, ya que su amplitud varia con la distancia al origen de la perturbación. Se puede demostrar que, en este caso, la impedancia acústica específica de una onda esférica viene dada por:
En el caso de que tengamos ondas planas armónicas la expresión sería:
La unidad de Intensidad en el Sistema Internacional es el W/m2. La intensidad mínima detectada por el oido humano es aproximadamente 10-12W/m2.
El valor eficaz de una magnitud representa algo que se puede medir.
La impedancia acústica en una determinada superficie se define como el cociente entre la presión eficaz promediada sobre la superficie y la velocidad de volumen efectiva a través de dicha superficie. La impedancia acústica representa la resistencia que el medio opone a que sus partículas se vean afectadas por el paso de la onda.
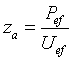
En el Sistema Internacional de Unidades, la unidad de impedancia acústica es el ohmio acústico o N s/m5.
La impedancia acústica específica es el cociente entre la presión sonora eficaz en un punto de un medio y la velocidad eficaz de desplazamiento de las partículas. Por lo tanto, la expresión matemática de la impedancia específia será: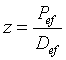 
En el Sistema Internacional de Unidades, la unidad de impedancia acústica específica es el Rayl o N s/m3; o también Km-2 s-1.
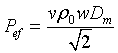
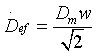
Por tanto, la impedancia z quedará: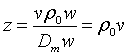 
En el caso de que tengamos ondas esféricas, la expresión de la presión va a ser ligeramente diferente, ya que su amplitud varia con la distancia al origen de la perturbación. Se puede demostrar que, en este caso, la impedancia acústica específica de una onda esférica viene dada por: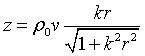 
En el caso de que tengamos ondas planas armónicas la expresión sería: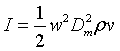 
La unidad de Intensidad en el Sistema Internacional es el W/m2. La intensidad mínima detectada por el oido humano es aproximadamente 10-12 W/m2.
Se denomina Potencia acústica de la fuente a la energía acústica que emite dicha fuente por unidad de tiempo. Se mide en watios. La potencia acústica de la fuente será: W=IS donde S es la superficie del frente de ondas que pasa por el punto situado s a una distancia r del foco.
Como el frente de ondas es esférico, tendremos que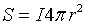 
. La fuente emite potencia y esta se manifiesta como presión sonora.
Hemos visto que mientras que para una onda plana su intensidad es constante, para una onda esférica la intensidad disminuye con la distancia al foco. Esto es válido siempre que no exista atenuación del sonido debido a las características del fluído en el cual se propaga la onda.
Las pérdidas en el medio son debidas fundamentalmente a tres factores: la viscosidad, conducción del calor y cambios moleculares.
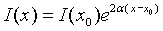
En los fluidos en movimiento aparecen fuerzas que se oponen al movimiento relativo entre capas contiguas, y que se denominan fuerzas de viscosidad. El coeficiente de viscosidad es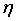 
. Se observa fácilmente que la atenuación no es la misma para todas las frecuencias. 
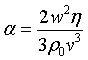Las frecuencias altas sufren una mayor disipación que las frecuencias bajas, especialmente para puntos alejados de la fuente sonora.
En general, la atenuación debida al calor de conducción es algo menor que la debida a la viscosidad, aunque del mismo orden de magnitud.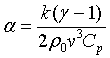 
.
El tercer factor en juego como causa de la disipación, la relajación térmica, supone una contribución muy pequeña la valor de la disipación total.