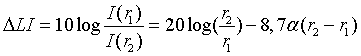Magnitudes acústicas (II)
Continuando con el post anterior ahora nos adentraremos en la superposición de las ondas acústicas. Supongamos que en un punto del espacio tenemos una serie de ondas acústicas armónicas que provienen de fuentes diferentes, y sin ninguna relación entre sí. La presión sonora resultante en dicho punto del espacio se obtendrá como la superposición de las presiones sonoras de dichas ondas, y tendremos, por lo tanto que: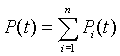 
.
La presencia de ondas diferentes en un punto del espacio da lugar a fenómenos de interferencia, que puede ser constructiva o destructiva dependiendo de la diferencia de fase entre las respectivas ondas. Así llegamos a la conclusión de que la intensidad total será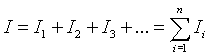 
.
En general, los sonidos que provienen de fuentes distintas son incoherentes, ya que para que dos ondas sean coherentes deben tener algún tipo de relación entre sí.
Ya hemos comentado que las intensidades mínima y máxima para el oído humano son, aproximadamente 10-12 W/m2 y 105 W/m2. Este es un rango de valores muy amplio y, por tanto, difícil de manejar. La ley de Weber-Fechner: La magnitud de la sensación percibida es proporcional al logaritmo del estímulo que la provoca, es decir: L = k logI donde L sería el nivel de sensación percibida, I es el valor del estímulo y k es una constante adimensional.
De esta manera podemos definir la escala de los Belios, donde los límites inferior y superior serán:
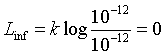
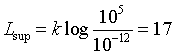
La escala de los belios se extiende desde 0 a 17 belios. La escala de Nivel de Intensidad más usada es la de decibelios, que resulta de usar una k=10, o, lo que es lo mismo, multiplicar por 10 la escala de belios.
.
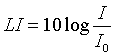El Nivel de presión de sonido medido en Decibelios se define como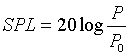 
donde P0 es la presión sonora de referencia y los valores de presión que estamos considerando son valores eficaces. Esta presión de referencia puede tomar dos valores:
1- P0 = 2 x 10-5 New/m2.
2- P0 = 0,1 New/m2.
El Nivel de Intensidad y el Nivel de Presión serán iguales si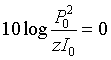 
. Si consideramos una impedancia característica del aire, p. ej., del orden de 400 rayl, y que la intensidad y presión de referencia son, respectivamente, 10-12 W/m2 y 2 x 10-5 New/m2, entonces LI = SPL.
El Nivel de Potencia de Sonido se define como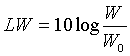 
donde W0 representará una potencia sonora de referencia.
En el caso de ondas esféricas, el proceso es ligeramente diferente.
Por tanto, en este capítulo hemos visto que conociendo el nivel sonoro en dB en un determinado punto del espacio, podremos también conocer la intensidad, presión o potencia sonora en ese punto.
Hemos visto anteriormente que si las ondas son incoherentes, la intensidad total del sonido será igual a la suma de las intensidades individuales.
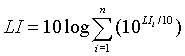
Vemos, pues, que dos sonidos incoherentes de igual intensidad se componen produciendo un sonido cuyo nivel de intensidad es 3dB más elevado que el de cualquiera de las dos ondas, o lo que es lo mismo, duplicar la intensidad de una onda equivale a aumentar en 3dB el nivel de intensidad total. Cuando existe una diferencia entre ambos niveles de 16dB, el nivel resultante es prácticamente igual al del sonido más fuerte.
Al duplicar la presión sonora en un punto se aumenta el nivel de presión en 6dB. Por lo tanto tendremos que: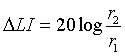 
.
Si doblamos la distancia, es decir si r2=2r1, tendremos que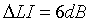 
. Cada vez que doblemos la distancia a la fuente se pierden 6dB de nivel intensidad, siempre que el medio sea no disipativo.
En el caso de que el medio sea disipativo tendremos que tener en cuenta la expresión ya indicada para ondas esféricas: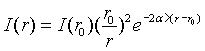 
.
Por tanto, para los dos puntos situados a r1 y r2 del foco, tendremos: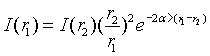 
Llegando finalmente a la conclusión: 