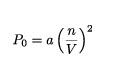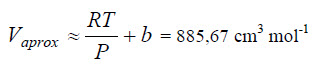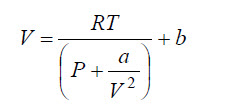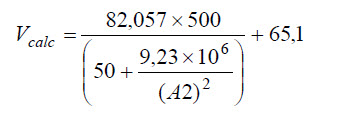Ecuación de Van der Waals
La ecuación de estado de un gas ideal no tiene en consideración dos hechos que están presentes en sistemas constituidos por gases reales (como oxígeno, azufre, entre otros);
- Las moléculas forman el gas y tiene volumen, por eso ocupan espacio
- Las moléculas poseen fuerzas de interacción entre ellas, siendo esencialmente fuerzas atractivas.
Siendo así, con el objetivo de corregir la ecuación del estado de un gas ideal, surge la ecuación de estado de Van der Waals.
La ecuación de Van der Waals permite describir de forma más satisfactoria el comportamiento termodinámico de muchos gases, no solo en altas temperaturas y bajas presiones, pero en un dominio más extenso de temperaturas y presiones nominadamente cuando el gas está próximo de la condensación.
Para corregirse el hecho de las moléculas tener volumen, se substituye en la ecuación del gas ideal, el volumen V por la cantidad:
V – nb
Donde b es el volumen ocupado por cada molécula que constituye el gas.
De esta forma, el volumen que el gas real puede ocupar es menor que la del gas ideal, una vez que las moléculas que constituyen el gas real tienen dimensión finita.
Con el objetivo de deducir el término asociado al hecho de que existan fuerzas de interacción entre las moléculas del gas, se considera un recipiente cerrado que contiene gas con una densidad de moléculas dada por el cociente n/V.
En la zona interior del recipiente, las fuerzas que actúan entre las moléculas son en promedio iguales a cero. Por otra parte, las moléculas que estén más en la periferia sienten una fuerza en la dirección del interior del recipiente.
Esto significa que la presión en un gas real Preal tiene que ser menor que la del gas ideal y para tener en cuenta ese hecho se sustituye en la ecuación del gas ideal, la presión P por la cantidad:
Preal + P0
Donde P0 se denomina como presión interior.
La presión interior no es simplemente una constante, desde que depende de la distancia media entre las moléculas y del número de moléculas que constituyen el gas.
En ambos casos estas dependencias son en primera aproximación, proporcionales a la densidad de moléculas n/V y puede asumirse que:
Introduciendo estas correcciones de la presión y del volumen, en la ecuación de estado del gas idea, se obtiene la ecuación de estado de Van der Waals. Las constantes a y b dependen del tipo de moléculas que constituyen el gas, siendo necesario determinarlas para cada gas (oxígeno, azufre, argón, etc) que se pretendan estudiar.
Uso de la Ecuación de Van der Waals
El Cálculo de las propiedades de un gas utilizando la ecuación de Van der Waals, o la ecuación de Redlich-Kwong o la ecuación virial, frecuentemente involucra la solución de una ecuación cúbica cuya solución puede ser muy trabajosa. Existen formas relativamente simples de resolverse este tipo de ecuaciones utilizando programas como Excel y utilizando como punto de partida una estimativa para la solución.
Vamos a considerar una situación en la cual se desea calcular el volumen molar del CH3OH gaseoso a una temperatura de 500K y 50 atm. Estos valores de presión y temperatura se encuentran por debajo de la temperatura crítica del metanol
(Tc = 512,5 K, Pc = 80,8 atm) y las constantes experimentales de la ecuación de Van der Waals para el metanol son:
a = 9,23×106 cm6 atm mol-2
b = 65,1 cm3 mol-1
Para utilizar un sistema de unidades consistente con las constantes de arriba, utilizamos:
R = 82,057 cm3 atm mol-1 K-1,
y el volumen molar en cm3 en la ecuación
Esta ecuación lleva a una ecuación cúbica en el volumen, cuya solución puede ser relativamente penosa. Una alternativa consiste en determinar inicialmente un valor aproximado para el volumen molar utilizando una ecuación más simple (ignorando el término adicional en la presión).
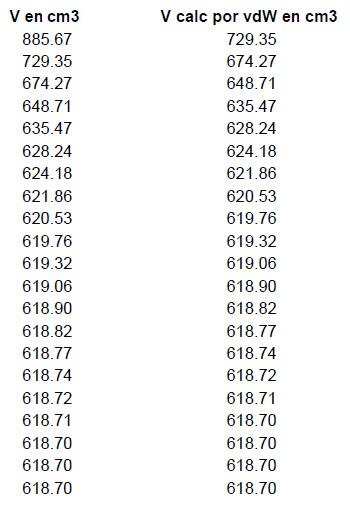
Este volumen inicial es lanzado en la celda A2 de la planilla Excel y en B2 entramos con la fórmula de la ecuación de Van der Waals
que para nuestro caso sería programado siendo:
Si la solución inicial fuera correcta, el valor de Vcalc debería ser igual a aquel que consta en A2. Como los valores son diferentes vamos a repetir esta operación hasta obtener concordancia entre el valor en la columna A y en la columna B.
Se comprueba que luego de 19 interacciones el resultado deseado es obtenido ya que el volumen utilizado en la columna A, corresponde a aquel que es calculado en B y por tanto el volumen molar del metanol (conforme Van der Waals)
V = 618,70 m3