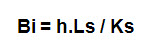Número de Biot
Estudiamos transmisión de calor con un objetivo en mente: el entendimiento de las características de los intercambios de calor entre dos o más cuerpos. Esto involucra el uso de principios básicos, la deducción de las ecuaciones fundamentales (Ley de Fourier, Ecuaciones de Conservación, etc), de las condiciones límites (o de contorno), etc. constituyendo el llamado modelo matemático que puede ser definido por ecuaciones algebraicas, diferenciales ordinales y parciales e integrales.
En tanto, aún que logremos describir adecuadamente los fenómenos físicos que nos interesan a través de un correcto modelo matemático, esto no se traduce automáticamente en que sepamos determinar la solución necesaria, muy por el contrario.
La complejidad de las situaciones de interés que necesitamos conocer y la consecuente complejidad de los móldelos matemáticos han impedido la obtención de las soluciones de forma sistemática.
Así, la experimentación hecha en laboratorios numéricos o físicos constituye una etapa importante en el entendimiento de los problemas.
El análisis dimensional es una herramienta poderosa para el planeamiento de experimentos, reduciendo significativamente su complejidad y con ello el costo de la experimentación, sea ella física o numérica y para la presentación de resultados experimentales, a través de la reducción matemáticamente organizada de los datos relevados.
Es claro, ellas no son mágicas y la comprensión y sus conclusiones no son garantía alguna de que los resultados de los experimentos serán mas o menos correctos y tampoco que la teoría que llevó a esos resultados sea la adecuada.
En otros artículos hemos hablado sobre estos conceptos y particularmente hemos citado algunos parámetros adimensionales como por ejemplo el número de Biot, el número de Fourier y otros.
Además de ello, el estudio de la convección se hace muy dependiente de estos parámetros: por ejemplo en número de Nusselt que relaciona el coeficiente de intercambio de calor por convección, h, el número de Grashof (para la convección natural), del número de Reynolds (para convección forzada) entre otros.
Número de Biot
El número de Biot (Bi) es un parámetro adimensional y representa la razón entre el coeficiente de transferencia convectiva de calor en la superficie del sólido y la conductancia específica de ese sólido.
La hipótesis de temperatura uniforme en el interior del sólido es válida si la conductancia específica del sólido es mucho mayor que el coeficiente de transferencia convectiva de calor.
Donde:
Ls = longitud característica Ls = V/A (volumen/área)
h = coeficiente convectivo de calor
Ks = Coeficiente conductivo de calor
El número de Biot es utilizado para definir el método a ser utilizado en la solución de problemas de transferencia de calor transitoria.
– Si Bi ³ 0,1 : se usan las cartas de temperatura transitoria
– Se Bi < 0,1 : se usa el análisis global, o sea
Entre otros aportes a la ciencia Jean-Baptiste Biot fue el primero en descubrir la única propiedad óptica de la mica y por tanto la biotita, un mineral basado en la mica, recibe este nombre en su homenaje. En 1804 Biot y Gay-Lussac construyeron un globo de aire caliente y subieron a más de 5 kilómetros de altura, la cual fue una de las primeras investigaciones realizadas sobre la atmósfera terrestre.