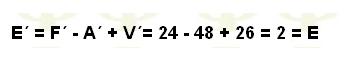El número de Euler
Nacido el 15 de abril de 1707, en Basil-Suiza, Euler fue sin duda el mayor matemático del siglo 18. Con 886 trabajos publicados, la mayoría de ellos al final de su vida, cuando ya estaba completamente ciego.
Euler ha sido importante no solo para la matemática, sino también para la física, ingeniería y astronomía ofreciéndonos conceptos como: Número de Euler, Números Eulerianos, Fórmula de Euler y cada uno de ellos significan cosas diferentes dependiendo del contexto.
En matemática, el número de Euler es la base de los logaritmos naturales. Las variantes del nombre del número incluyen: Número de Napier, constante de Nepere, número Neperiano, contante matemática y número exponencial, etc.
La primera referencia a la constante fue publicada en 1618 en la tabla de un apéndice en un trabajo sobre logaritmos de John Napier. Sin embargo, este no contiene la constante propiamente dicha, sino apenas una simple lista de logaritmos naturales calculados a partir de esta.
La primera indicación de la constante fue descubierta por Jakob Bernoulli, cuando intentaba encontrar un valor para la siguiente expresión:
Y su valor aproximadamente es de : 2,718281828459045235360287.
El número, es un número irracional e inclusive tan trascendente como p la irracionalidad de e fue demostrada por Lambert en 1761 y más tarde por Euler. La prueba de la trascendencia de e fue establecida por Hermite en 1873.
Se ha conjeturado sobre e que es un número normal o aleatorio. El aparece (junto a otras constantes fundamentales) en la identidad de Euler:
La topología de Euler
Este gran matemático, fue para quien inauguró una rama de las matemáticas denominada topología. Ahora expondremos uno de los teoremas topológicos de Euler.
Consideremos un objeto tridimensional bien sencillo: un cubo. El cubo tiene 6 caras, 12 aristas y 8 vértices. Llamaremos al número de caras F, al número de aristas A y al número de vértices V.
Tomando en cuenta la definición del número de Euler (e) tendremos que:
Por tanto el número de Euler del cubo será:
E(del cubo) = 6 – 12 + 8 = 2
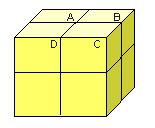
E teorema de Euler dice que el número de Euler es constante para una superficie cualquiera. Esto quiere decir lo siguiente: supongamos que dividimos las caras del cubo en 4 partes, trazando 2 segmentos de recta perpendiculares entre sí, como vemos en la figura:
Ahora, puntos como (A) o (B) serán considerados nuevos vértices, líneas como (AB) serán nuevas aristas y áreas como (ABCD), nuevas caras.
Entonces contemos los nuevos valores de caras, aristas y vértices. Luego de la división obtendremos 24 caras, 48 aristas y 26 vértices, entonces el número de Euler de esta figura será:
El resultado es el mismo que antes. Y aún si dibujaramos sobre el cubo una serie de líneas irregulares sin sentido, creando una gran cantidad de nuevas aristas, vértices y cadas, obtendremos siempre el mismo valor: 2.
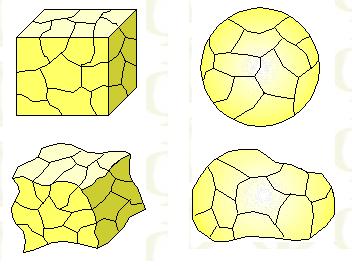
No nos admiraremos aún cuando hubiéramos deformado el cubo de tal forma como mostramos en la figura, porque aunque lo desfiguremos y en vez e un cubo se pareciera más a una esfera, el número de Euler continuaría incambiado.
Técnicamente se dice que el cubo y la esfera son superficies topológicamente idénticas. Todas poseen el mismo número de Euler : 2.
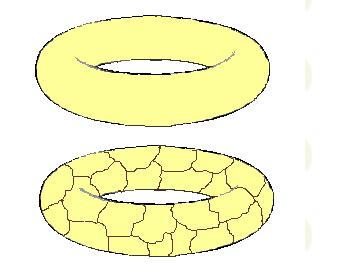
Las consideraciones cambian en el caso que el objeto tuviese un agujero. El objeto agujereado más citado por los matemáticos es el toro o toroide.
Si sobre la superficie del toroide hacemos lo mismo que sobre el cubo anteriormente citado y luego hacemos las cuentas, tendremos que el numero de Euler en un toroide es nulo o sea, igual a 0.
El toroide y cualquier superficie con un agujero es topológicamente diferente del cubo y la esfera. No se puede transformar una esfera en un toroide sin cortar o rasgar alguna parte.
Tal vez nos parezca extraño que el toroide tenga curvatura cero, cuando a simple vista parece bastante curvado. Es obvio que la curvatura local del toroide no es 0 en todos los puntos. Lo que es igual a 0 es la curvatura total del toroide.
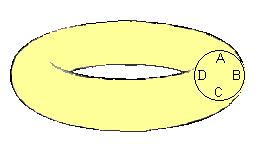
Consideremos un corte en el toroide que resulta en el círculo ABCD. Los puntos que quedan del lado de fuera (ABC), menos los extremos A y C tienen curvatura positiva. Los puntos que quedan del lado de adentro (ADC) tienen curvatura negativa. Y los puntos A y C tienen curvatura nula. Computando todo, encontramos que la curvatura total es igual a cero.
Cuando la superficie tiene agujeros, la expresión para el número de Euler acaba siendo:
E = F – A + V = 2 – 2 x B
siendo B el número de agujeros u hoyos en la superficie. Para una esfera o un cubo, B=0, E=2. Para un toroide, B=1 y E = 0. Con más de un agujero u hoyo, el número de Euler se vuelve negativo.
Y cual es la relación entre el número de Euler y la curvatura de Gauss?
LA CURVATURA DE GAUSS E O NÚMERO DE EULER
La curvatura de Gauss (G) y el número de Euler (E) están vinculadas por el conocido Teorema de Gauss-Bonnet que presenta:
Como recordamos , B es el número de agujeros en la superficie. Para una esfera B = 0, E = 2 y G = 4. Para un toroide, B=1, E=0 y G=0.
La maravilla de este teorema es que el enlaza una propiedad geométrica, la curvatura de Gauss, con una propiedad topológica, el número de Euler. Y todo de una forma muy simple.
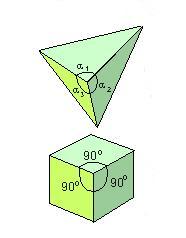
Para apreciar mejor el significado de este teorema, utilicemos un modelo de pirámide de tres caras.
Primero medimos los tres ángulos de la cara con un semicírculo (transferidor) y sumamos los tres. Luego calculamos cuanto le falta a esa suma para completar 360º. Ese valor será llamado ángulo faltante. Esto es, el ángulo faltante en el vértice de la pirámide es:
Δ = 360 – (α1 + α2 + α3)
Si practicamos esto mismo en el vértice de un cubo, encontraremos que:
Δ = 360 – (90 + 90 + 90) = 90º = p/2
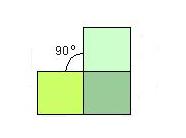
Ese resultado para el ángulo faltante en el vértice del cubo queda más claro si nosotros cortamos una arista y esparcimos los tres lados sobre una mesa como mostramos a continuación:
Por tanto, el ángulo faltante en cada vértice del cubo es p/2. El ángulo faltante total (que llamarmos T), para el cubo será por tanto 8 x p/2 = 4p. Ese valor como ya sabemos mide la curvatura de Gauss del cubo. Y esto vale no solo para el cubo, sino para cualquier objeto geométrico, por lo tanto el teorema de Gauss Bonett puede ser resumido como:
“El ángulo faltante de una superficie es igual a la curvatura de Gauss de esa superficie”