Una de momentos (I) – Momento de una fuerza, momento lineal e impulso
Hablemos de los distintos momentos de traslación que encontramos en la dinámica de una partícula o de un sistema.
Escribiremos el producto escalar con un punto (·), y el producto vectorial con una cruz (x). Las magnitudes en negrita son vectoriales y las que no están en negrita son escalares.
Momento de una fuerza (M):. 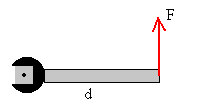
Se denomina momento de una fuerza respecto de un punto, al producto vectorial del vector posición r de la fuerza por el vector fuerza F.
M=r x F
Por lo tanto el módulo de M es: M = F x r = F · rsenα = F · d siendo d la distancia del origen a la dirección de la fuerza y r el vector de posición de donde se aplica la fuerza. Normalmente, como es el caso típico de un tornillo o una palanca, la fuerza se aplica en el extremo de la herramienta así que el seno del ángulo entre la dirección de F y la dirección de r es 1 (porque α es cero y sen 0=1) y entonces r=d.
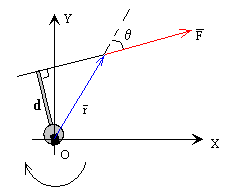
Momento lineal (P):
También llamado cantidad de movimiento. Su ecuación es: P = m x v. Como ya veíamos en la segunda ley de Newton, F = δP / δ t. Su dirección es tangente a la trayectoria del movimiento en cada punto y tiene el mismo sentido que la velocidad (v).
Se dice que un observador inercial es aquel para el que una partícula libre mantiene constante su cantidad de movimiento. Si la cantidad de movimiento es constante implica que su derivada es cero, por lo tanto la fuerza es cero. Así que reescribimos la frase anterior a: un observador inercial es aquel para el que no percibe que ninguna fuerza externa actúe sobre una partícula libre. De esto deducimos el:
Principio de conservación del momento lineal:
«Si sobre un sistema no actúa ninguna fuerza externa o la suma de las fuerzas vale 0, su momento lineal es constante».
Es decir, que antes y después de un choque, por ejemplo, debe existir el mismo momento lineal. Por lo tanto la m x v (al inicio) = m x v (al final). Por lo tanto, si en el choque, el objeto se rompe y se separa en piezas, el resultado «al final» es la suma de cada masa multiplicada vectorialmente por su vector velocidad (ya que cada trozo llevará una velocidad distinta).
En un sistema de partículas (donde hay más de una), la cantidad de movimiento del centro de masas coincide con la suma de las cantidades de movimiento de cada punto material. Y está comprobado que también se cumple el principio de conservación, pues, en ausencia de fuerzas externas, la cantidad de movimiento total es constante ya que las fuerzas internas se anulan entre sí y no lo modifican.
Impulso (I):
Esto no es un momento, sino la diferencia de momentos. Se define como el producto de una fuerza aplicada a una masa durante un tiempo t. Es decir, la diferencia de momentos lineales pasado un tiempo. Si I=F·t y F=m·a –> I=m·a·t. Y a=(v–v0)/t, por lo tanto I=m((v–v0)/t)·t –> I=mv-mv0=P–P0.
