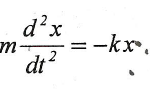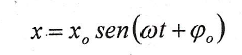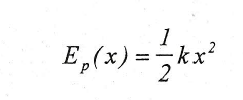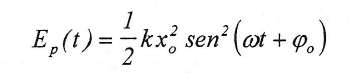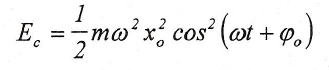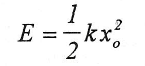Movimiento armónico simple
Decimos que un cuerpo describe un movimiento armónico simple (MAS) en la dirección del eje X cuando se halla sometido a una fuerza del tipo: F=-kxi; siendo k una constante y x=0 la posición en la que la fuerza se anula o posición de equilibrio. Según la ecuación anterior, la fuerza se opone al desplazamiento del cuerpo de la posición de equilibrio.
De acuerdo con la segunda Ley de Newton: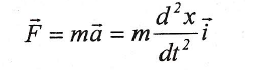
Por tanto, la ecuación de un MAS en la dirección del eje X es:
Se puede comprobar fácilmente, que la solución para la ecuación de un MAS es:
Donde: x es la elongación o distancia del cuerpo a la posición de equilibrio en el instante t; xo es la amplitud del movimiento o elongación máxima; ω es una constante denominada frecuencia angular; ( ωt-φo) es la fase del movimiento; y φo la fase inicial.
El valor de la frecuencia angular ( ω) es:
Realizando la primera derivada de x en función de t obtenemos la velocidad; y volviendo a derivar, la aceleración del cuerpo:
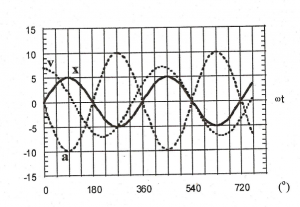
Lo cual, unido a la solución para la ecuación de un MAS, pone de manifiesto el carácter periódico del MAS. Por tanto, si representamos en un mismo gráfico las tres magnitudes en el caso de la fase inicial cero: posición (x), velocidad (dx/dt) y aceleración; como en la siguiente imagen. Podemos observar que no alcanzan los valores máximos o mínimos en le mismo instante. La velocidad se anula cuando la elongación es máxima, y viceversa; porque presentan una diferencia de fase de 90º (se dice que están en cuadratura). La elongación y la aceleración presentan en los mismos instantes valores nulos y máximos de signo opuesto porque su diferencia de fase es de 180º (se dice que están en posición).
Además también se puede apreciar como las tres gráficas se repiten exactamente cada 360º, es decir, cada T=2π/ ω segundos, lo cual constituye el periodo del movimiento.
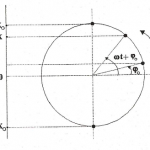El MAS guarda una estrecha relación con el movimiento circular uniforme. Como podemos ver en la siguiente imagen, donde se muestra cómo la proyección sobre un diámetro de la posición de una partícula que describe un movimiento circular obedece la ecuación de la posición x. Es decir, la proyección sobre un diámetro de la posición de una partícula que gira a una velocidad angular constante describe un MAS.
Fuerzas recuperadas de la forma F= -kxi, las cuales originan un MAS, se presentan por ejemplo al estirar o comprimir un muelle (ley de Hooke) o al desplazar ligeramente un péndulo de su posición de equilibrio.
ENERGÍA EN EL MOVIMIENTO ARMÓNICO SIMPLE
La fuerza del tipo F= -kxi es conservativa y le corresponde una energía potencial tal que: -dEp= Fdr, por tanto:
Tomando Ep=0, para x=0, la constante de integración es cero y nos queda:
Esta última ecuación es el valor de la energía potencial de un oscilador armónico simple que se encuentra desplazado una distancia x de la posición de equilibrio. Luego la energía potencia en función del tiempo es:
La energía cinética del oscilador es:
La energía mecánica total, que se obtiene al sumar la potencial y la cinética: E=Ec+Ep es:
