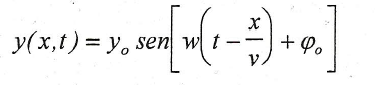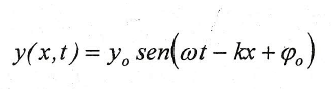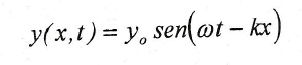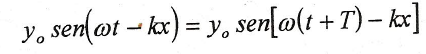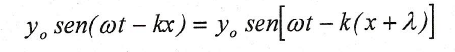Ondas armónicas
Una vez que nos hemos familiarizado con el movimiento armónico simple, vamos a continuar describiendo el resultado de este tipo de movimientos: las ondas armónicas.
Definición: Llamamos onda armónica a la onda generada en un movimiento armónico simple. Aparece cuando tensamos una cuerda por un extremo haciendo describir al otro extremo un MAS en dirección perpendicular.
Si tomamos el extremo libre como origen de coordenadas, el desplazamiento de la posición de equilibrio vendrá dado por:![]()
donde ω es la frecuencia angular de la perturbación armónica y φo la fase inicial.
Este movimiento se transmite a las porciones adyacentes de la cuerda con velocidad υ gracias a su elasticidad e inercia, de modo que una partícula situada a una distancia x del extremo libre sufre un desplazamiento:
Teniendo en cuenta que x/υ es el tiempo que la perturbación tarda en alcanzarla, obtenemos la ecuación que describe el estado de vibración de los puntos del medio situados a una distancia x del origen en el instante t:
donde k= ω/υ es una determinada característica de la onda denominada número de ondas. Por simplicidad, tomaremos de ahora en adelante nuestra fase inicial como 0: φo=0; con lo que la ecuación que describe una onda armónica que se propaga a lo largo del eje +X con velocidad υ= ω/k es:
Observación: Para hallar la ecuación que describe a lo largo del eje -X, sólo tendríamos que cambiar el + por el -.
El movimiento ondulatorio representado por la ecuación anterior es doblemente periódico, tanto en el tiempo como el espacio:
a) En el tiempo:
Una partícula determinada del medio (x fija) describe un MAS de frecuencia angular ω y periodo T de forma que:
sustituyendo en la ecuación de la onda:
Por tanto ωT=2Π y cada T= 2Π/ω segundo la partícula describe una oscilación completa, o lo que es lo mismo, en un segundo habrá realizado f=1/T oscilaciones. Esta magnitud, f, se denomina frecuencia de la onda y se mide en herzios (Hz) en el SI.
b) En el espacio:
Si en un instante determinado (t fijo) observamos el medio por el que se propaga la onda encontraremos a las partículas en diferentes estados de vibración. La distancia entre dos puntos consecutivos que oscilan en fase se denomina longitud de onda (λ), por lo que:
Es decir:
Que en este caso nos lleva a: k λ=2Π o bien λ=2Π/k en un instante dado, todos los puntos del medio alcanzados por una onda y distantes entre sí un número entero de longitudes de onda se encontrarán oscilando en fase:
Observación: Todo lo mencionado anteriormente puede utilizarse también cuando sustituimos en la ecuación de la onda la función seno por la función coseno, ya que el cambio simplemente supondría una corrección en la fase de Π/2 radianes.