Formalismo de Lagrange

Todos conocemos las 3 famosas leyes de Newton (1642-1727): sobre ellas se basó la física mecánica durante mucho tiempo. Ésta manera de concebir la mecánica está regida principalmente por su carácter vectorial y la segunda ley de Newton: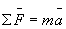 . Pero como todo método, también tiene sus inconvenientes. Resolver un problema mediante “Newton” puede llegar a ser extremadamente difícil en sistemas complejos, como por ejemplo péndulos suspendidos sobre cuerpos en movimiento, partículas sometidas a moverse sobre superficies cónicas, etc… Obviamente estos problemas también pueden ser resueltos por el método de Newton (no vamos a quitarle méritos), pero nos llevaría a integrales de extrema complejidad.

Aquí es donde aparece Joseph-Louis de Lagrange (1805-1865). Italiano de nacimiento pasó gran parte de su vida arraigado en Francia, considerándosele aún hoy en día por éstos, como compatriota suyo a pesar de lo que digan los demás. Todo lo que vamos a tratar está recogido en su obra Mecanique Anlitique.

Su formalismo se basa en las ligaduras, en la ausencia del carácter vectorial y en la simpleza en los cálculos. Pasamos ahora a un estudio más exhaustivo, pero directo, de su formalismo:

-Ligaduras: condición que se impone a un sistema limitando el movimiento de éste.

Ejemplos:

Partícula en una circunferencia: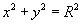

Partículas en el plano: z=0

Habiendo definido las ligaduras llegamos al concepto de coordenadas independientes:

Las coordenadas independientes o generalizadas ( q_j ) son aquellas que su valor no depende de ninguna otra coordenada en el plano y desde las cuales describiremos el movimiento a estudiar. Ejemplo:

En un péndulo simple podemos tomar como coordenada generalizada el ángulo θ respecto a la horizontal.

De la misma manera que hablamos de coordenadas generalizadas podemos hablar de fuerzas generalizadas ( Q_j ) y velocidades ( 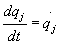) o aceleraciones generalizadas ( ).

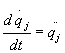En cada caso podemos establecer el número de coordenadas independientes como:

nº coordenadas independientes = nº coordenadas- nº ligaduras

Ahora definiremos una función muy importante a lo largo de la física: la Lagrangiana.

L=T-V siendo T la energía cinética y V la energía potencial

Definida la Lagrangiana podemos ver como hallar las ecuaciones de movimiento de esta manera:

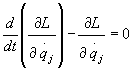
Cabe decir que ésta ecuación es sólo válida para sistemas conservativos (E=cnte=T+V), que aunque son minoría en la naturaleza son los más estudiados.

Vemos que la ventaja de este método estriba en la ausencia del carácter vectorial, y en la simpleza tanto matemática como formal de conseguir las ecuaciones que rigen el movimiento. La mayor dificultad será pues elegir las coordenadas con las que vamos a trabajar (cartesianas, cilíndricas, esféricas…) Los pasos a seguir serán:

• Elección coordenadas

• Elección coordenadas generalizadas

• Deducción de ligaduras

• Hallar la T ( 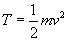) y V para construir la L

• Derivar L para hallar las ecuaciones de movimiento

• Resolver las ecuaciones de movimiento (si se estima necesario)

En siguientes artículos podremos ver la ampliación de este método por Hamilton, o el principio de Hamilton, por el cuál se rigen todos los fenómenos en la naturaleza.