Oscilaciones lineales
Entendemos por oscilador lineal el sistema en que una partícula se desplaza de su posición en una sola coordenada. Véase por ejemplo un muelle, un péndulo, etc…
Para estudiarlos desarrollamos un potencial cualquiera V en una serie de Taylor: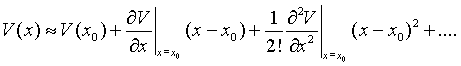
Moviendo l origen de potenciales hacemos cero el primer término y el segundo se hace cero por definición ya que es una posición de equilibrio. De esa manera obtenemos que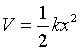 
y sabiendo que 
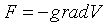obtenemos la ley de Hook: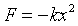 
Ahora según el número de fuerzas que actúan sobre nuestra partícula podremos distinguir distintos tipos de osciladores:
-oscilador armónico simple:
Fuerzas: F=-kx
Por la segunda ley de Newton obtenemos la ecuación de movimiento: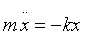 
haciendo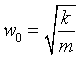 
obtenemos 
.
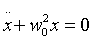La solución de esta ecuación se puede escribir como: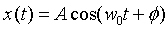 
Se trate de un sistema conservativo, por lo tanto T+V=cnte donde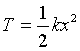 
y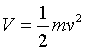 
-oscilador amortiguado
Fuerzas: F=-kx y la fuerza de rozamiento F=-bv
Será la ecuación de movimiento por tanto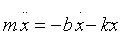 
y haciendo 
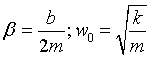obtendremos que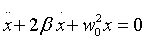 
Resolviendo debemos distinguir 3 casos:
• Inframortiguado: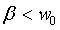 
Se define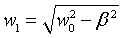 
y la solución de la ecuación es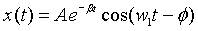 
• Amortiguamiento crítico: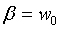 
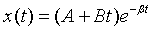
• Sobreamortiguado: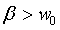 
Se define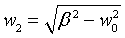
y la solución de la ecuación es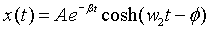 
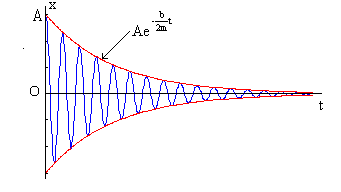
En todos los casos la amplitud decae con el tiempo de forma exponencial.
-Oscilaciones forzadas
Fuerzas: F=-kx ; F=-bv ; Y la fuerza que aplicamos nosotros al oscilador que puede ser de cualquier tipo, por ejemplo F=fcoswt
La ecuación de movimiento será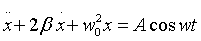 
La solución de esta ecuación no es tan trivial como las anteriores pero omitiré su resolución. Esta solución es: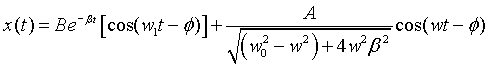 
La primera parte de la solución representa los efectos transitorios, ya que a medida que avanza el tiempo este término se hace nulo. El segundo término representa los efectos transitorios.
Para que se produzca resonancia en amplitud (amplitud máxima) la frecuencia ha de ser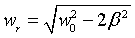 
. Para que halla resonancia en energía cinética 