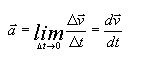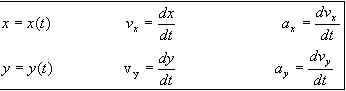Movimiento curvilíneo

Llamamos movimiento curvilíneo al movimiento que realiza una partícula o un móvil que sigue una trayectoria parabólica, elíptica, vibratoria, oscilatoria o circular.

Las magnitudes que utilizamos para describir un movimiento curvilíneo son las siguientes:

-Vector posición: sabemos que la posición en la que se encuentra una partícula o un móvil depende del tiempo en el que nos encontremos, es decir, que varía en función del tiempo. Por tanto, como podemos observar en la siguiente imagen, la partícula se encuentra en el punto P cuando estamos en el instante t, y su posición viene dada por el vector r.

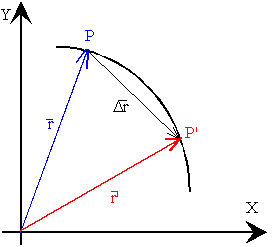-Vector desplazamiento: Cuando nuestra partícula pasa de estar en el punto P en el instante t, al punto P´en el instante t´, diremos que ésta se ha desplazado, y lo indicamos con el vector Dr , que como podemos observar en la imagen anterior, es el vector que une P y P´.

-Vector velocidad media: llamamos velocidad media al cociente entre el desplazamiento y el tiempo que emplea en desplazarse, es decir:

Tanto el vector de la velocidad media, como el vector desplazamiento tienen la misma dirección.

– Vector velocidad instantánea: Este vector se obtiene al hacer el límite cuando el Dt tiende a cero:

Este vector es tangente en el punto P a la trayectoria que sigue la partícula.

– Vector aceleración media: De forma similar al caso de la velocidad media, la aceleración media es igual al cociente entre el incremento de velocidad y el incremento del tiempo:

-Vector aceleración instantánea: Es el vector obtenido al hacer el límite cuando Dt tiende a cero:

ECUACIONES DE UN MOVIMIENTO CURVILÍNEO

Teniendo en cuenta que en el plano XY un movimiento curvilíneo viene determinado por la componente del eje x y por la componente del eje y. Entonces, escribimos las ecuaciones de un movimiento curvilíneo como podemos ver en la siguiente imagen. Donde x indica el desplazamiento de una partícula, t el tiempo, v la velocidad y a la aceleración.

EJEMPLO

Para finalizar la explicación resolveremos como ejemplo dos problemas de movimiento curvilíneo, el primero de ellos bastante facilito, mientras que en el segundo debemos poner en práctica muchos de los conceptos adquiridos:

Problema 1: Sabemos que un automóvil describe una curva plana. Calcular las componentes de la velocidad y de la aceleración en cualquier instante sabiendo que su trayectoria viene determinada por las siguientes expresiones:

Las componentes de la velocidad en cualquier instante.

Las componentes de la aceleración en cualquier instante.

Problema 2: Lanzamos una pelota de forma vertical hacia arriba con una velocidad de 30m/s desde la azotea de un edificio que tiene una altura de 60m. Sabemos que la pelota es empujada por el viento, de tal forma que se produce un movimiento horizontal con una aceleración de 3m/s2. A partir de estos datos calcular:

a) La distancia horizontal entre el punto de lanzamiento y el punto donde caiga.

b) La altura máxima que alcanza la pelota.

c) La componentes de la velocidad y el instante en el que la pelota se encuentra a 70 m de altura.

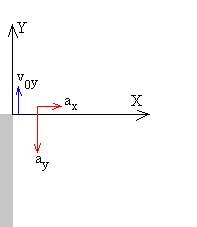En primer lugar, realizamos un esquema estableciendo las magnitudes de nuestro movimiento, tomando como referencia la azotea del edificio.

A continuación analizamos los datos que nos da el problema:

A partir de los datos planteamos la ecuaciones del problema:

– Movimiento uniformemente acelerado a lo largo del eje X:

-Movimiento uniformemente acelerado a lo largo del eje Y (movimiento de caída de los cuerpos):

a) El punto de impacto con el suelo tiene coordenada x desconocida, pero sabemos que y=-60m. A partir del valor de y, podemos obtener el valor de t, resolviendo la ecuación; y luego el de x: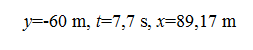

b) Para hallar la altura máxima de la pelota, tenemos que tener en cuenta que se produce cuando la velocidad vertical es cero:

Por tanto la altura desde el suelo será: 60+45,9=105,9 m.

c) En primer lugar hallamos el instante en el que ocurre esto, teniendo en cuenta que el móvil se encontrará en dos instantes a 70m sobre el suelo, (10 sobre el origen), y=10m, por tanto tenemos dos soluciones para la ecuación de segundo grado:

Sustituyendo:

Si t=0,59s; vx=1,77 m/s; vy=24,22 m/s

Si t=3,41s; vx=10,23 m/s; vy=-3,41 m/s